Page 97 - 应用声学2019年第5期

第 38 卷 第 5 期 张海如等： 基于并行蚁群算法的长基线定位方法 849

每一代蚁群的子个体数为 P = 40，θ = 500。对站 式 (2) 可能获得局部最优解，采用 PACA 方法获得
点 4 的第 1 个发射点，PACA 的第一个子系统求解 的目标位置估计值更接近适应度函数的全局最优
表达式 (2) 对应的目标函数收敛曲线如图 3 所示。 解。由于单个子系统求解表达式 (2) 的收敛速度较
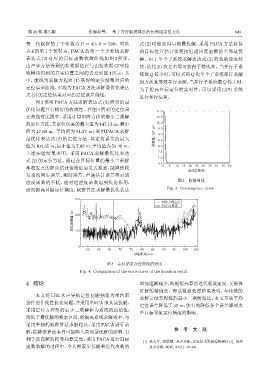
由声学方法得到的接收船位置与由接收船 GPS 接 快，迭代 20 次左右即可获得平稳残差。当并行子系
收模块得到的真实位置之间的误差如图 4 所示，其 统数 Q 较小时，可以采用 Q 次单个子系统串行求解
中，虚线为求解方程组 (1) 获得的定位结果对应的 的方法来等效并行求解；当并行子系统数 Q较大时，
定位误差曲线，实线为 PACA 方法求解最优化表达 为了提高目标定位的实时性，可以采用 GPU 系统
式 (2)的定位结果对应的定位误差曲线。
进行并行运算。
图 3 表明 PACA 方法求解表达式 (2) 所示的最
优化问题具有较好的收敛性。在图 4 所示的定位误 11.0
差曲线对比图中，采用计算矩阵方程的最小二乘解 10.5
的定位方法，其定位误差的最大值为147.13 m、最小 10.0
值为 47.60 m、平均值为 81.37 m；采用 PACA 求解 9.5
9.0
最优化表达式 (2) 的定位方法，其定位误差的最大 ឨࣀϙ/10 6 m 2 8.5
值为104.35 m、最小值为7.09 m、平均值为50.46 m。 8.0
上述实验结果表明，采用 PACA 求解最优化表达 7.5
7.0
式 (2) 的定位方法，通过在目标位置的最小二乘解
6.5
和收发点的距离估计值附近启发式搜索，能降低收 0 5 10 15 20 25 30 35 40 45 50
ᤖ̽൓஝ ൓
发系统同步误差、测时误差、声速估计误差等对适
应度函数的干扰，能对适应度函数起到优化作用， 图 3 收敛曲线
进而提高目标定位精度；蚁群算法求解最优化表达 Fig. 3 Convergence curve

150
ᅾ᫼வሮࠀͯ
PACAࠀͯ
ࠀͯឨࣀϙ/m 100

50

0
55 60 65 70 75 80 85 90 95 100 105
࠮ᓈᡰሏ/km
图 4 定位结果误差曲线的对比

Fig. 4 Comparison of the error curve of the location result

4 结论 增加逐渐减小，既能提高算法迭代收敛速度，又能保
证解的精确度。海试数据处理结果表明，与传统的
本文将 LBL 水声导航定位问题抽象为带约束
求解定位方程组的最小二乘解相比，本文方法平均
条件的非线性优化问题，并采用PACA求其最优解。
定位误差降低了30 m，能有效降低各个误差源对水
采用定位方程组的最小二乘解作为系统的初始值，
声目标导航定位精度的影响。
降低了最优解的搜索区间，能提高系统求解效率；与
采用单独的蚁群算法求解相比，采用 PACA 进行求
参 考 文 献
解，能降低算法本身可能陷入局部最优解的影响，有
利于提高解的精度和稳定性；采用 PACA 进行目标
[1] 孙大军, 郑翠娥. 水声导航、定位技术发展趋势探讨 [J]. 海洋
函数求解的过程中，令其搜索步长随着迭代次数的 技术学报, 2015, 34(3): 64–68.