Page 41 - 《应用声学》2019年第6期

第 38 卷 第 6 期 王玉龙等： 超声速弹丸立靶弹着点定位模型研究 943

10 T10 -3
18
9
16
8 0.04
14
7 0.02 12
ᰴͰ/m 6 ឨࣀ/m 0 10
5
-0.02 8
4 6
-0.04
3 10 4
10 2
5
2 ඵࣱ/m 5
ᰴͰ/m 0
1 0 0
0 1 2 3 4 5 6 7 8 9 10
ඵࣱ/m (a) ۳వവی
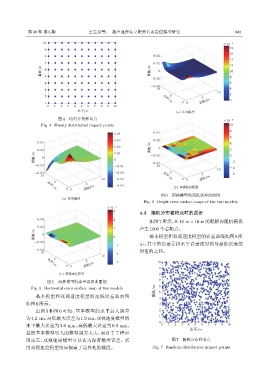
图 4 均匀分布弹着点
T10 -5
Fig. 4 Evenly distributed impact points 10
8
0.04 0.04
6
0.03 0.02
0.04 4
0.02 ឨࣀ/m 0
0.02 0.01 2
ឨࣀ/m 0 0 -0.02 0 -2
-0.02 -0.01 -0.04
10
10 -4
-0.04 -0.02 5 5 -6
10 ඵࣱ/m
10 -0.03 0 0 ᰴͰ/m
5 5
ᰴͰ/m -0.04 (b) ԥ᜽ᤴएവی
ඵࣱ/m
0 0
图 6 两种模型的高低误差曲面图
(a) ۳వവی
Fig. 6 Height error surface maps of the two models
T10 -3
3
4.3 随机分布着靶点时的误差
0.04 2
如图7所示，在10 m × 10 m的靶幅内随机模拟
0.02 1 产生1000个着靶点。
ឨࣀ/m 0 0 基本模型和双视速度模型的误差曲线如图8 所

-0.02 示，其中的误差是指水平误差绝对值与高低误差绝
-1
-0.04 对值的之和。
10 -2
10
5 5
ᰴͰ/m -3 10
ඵࣱ/m
0 0
9
(b) ԥ᜽ᤴएവی 8
图 5 两种模型的水平误差曲面图 7
Fig. 5 Horizontal error surface map of two models ᰴͰ/m 6 5
基本模型和双视速度模型的高低误差曲面图
4
如图6所示。 3
由图 5 和图 6 可知，基本模型的水平最大误差 2
为4.2 cm，高低最大误差为1.9 cm；双视速度模型的 1
0
水平最大误差为 3.0 mm，高低最大误差为 0.3 mm。 0 1 2 3 4 5 6 7 8 9 10
ඵࣱ/m
显然基本模型引入的模型误差太大，而对于工程应
用而言，双视速度模型可以认为没有模型误差。采 图 7 随机分布弹着点
用双视速度模型明显提高了边界处的精度。 Fig. 7 Random distribution impact points