Page 89 - 《应用声学》2019年第6期

第 38 卷 第 6 期 钱骥等： 基于 ARX 系统辨识模型的钢绞线张拉力识别 991

拉力指标I stf ，结果如图6所示。 变化规律。传感器布置在端面时，最小二乘法直线
2
基于 6组独立的钢绞线逐级加载数据构建的张 拟合 k = −5.93，确定系数 R = 0.984，传感器布置
拉力识别指标I stf 随张拉力增大呈现出明显的单调 在侧面时 k = −5.46，确定系数 R = 0.933。相比
2
变化规律。由于指标值 I stf 是以 70%F m 作为基准 较于侧面布置传感器，传感器布置在端面时，拟合
值，荷载越小将产生更大的模型参数差异，从而识别 直线斜率 k 值绝对值增大了 8.6%，确定系数增大了
指标值也将更大，所以关系曲线表现为负斜率。考 5.5%。k 值减小将使得在同样的应力变化条件下，识
虑到运营期结构的实际受力状态，实验数据没有考 别指标值的变化更为明显。
虑20%F m 以下的受力状态。
3.0 K/֓⊲ ቫ᭧ᝠካፇ౧

3.0 ኄʷጸ 2.5 R /⊲ Ο᭧ᝠካፇ౧
ቫ᭧લՌజጳ
ኄ̄ጸ सઢҧគѿૉಖ I stf 2.0 Ο᭧લՌజጳ
सઢҧគѿૉಖ I stf 2.0 ኄ̋ጸ 1.5 K/֓⊲
ኄʼጸ
2.5
ኄپጸ
ኄОጸ
1.0
1.5
લՌజጳ
0.5
1.0

R /⊲
K=-5.59
0
0.5
2
R =0.964
0.2 0.3 0.4 0.5 0.6 0.7
0
सઢҧ F m
0.2 0.3 0.4 0.5 0.6 0.7
सઢҧ F m
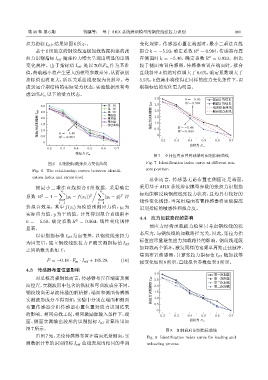
图 7 不同位置布置传感器时识别指标曲线
图 6 识别指标随张拉力变化曲线 Fig. 7 Identification index curve at different sen-
sors position
Fig. 6 The relationship curves between identifi-
cation index and stress level
总体而言，传感器无论布置在侧面还是端面，
按最小二乘法直线拟合 6 组数据，采用确定 采用基于 ARX 系统辨识模型参数的张拉力识别指
n / n
∑ ∑ 标均能够反映钢绞线张拉力状态，且均具有较好的
2 2 2
系数 R = 1 − (y i − f(x i )) (y i − ¯y) 评
线性变化规律，当采用端面布置传感器将更能提高
i=1 i=1
价拟合效果，其中 f(x i ) 为模型预测应力值，y i 为 识别指标的敏感性和拟合度。
实际应力值，¯y 为平均值。计算得到拟合直线斜率
4.4 应力加载路径的影响
2
k = −5.59，确定系数 R = 0.964，线性变化规律
预应力结构承载能力检算只考虑钢绞线的状
显著。
态应力，与钢绞线的加载路径无关，因此，张拉力指
以识别指标值 I stf 为自变量，以钢绞线张拉力
标值应尽量避免应力加载路径的影响。钢绞线逐级
为因变量，建立钢绞线张拉力 F 随实测指标值 I stf
加卸载两个循环，激发同样的宽频单周期正弦脉冲，
之间函数关系如下：
端面布置传感器，计算张拉力指标值 I stf 随加载等
F = −0.18 · F m · I stf + 185.28. (16) 级变化如图8所示，直线拟合参数如表3所示。
4.3 传感器布置位置影响
3.0 ኄʷ൓ҫᣒ
对单根高强钢丝而言，传感器布置在端面及侧 2.5 ኄʷ൓ԅᣒ
面位置，实测波形中包含的纵波和弯曲波成分不同。 2.0 ኄ̄൓ҫᣒ
ኄ̄൓ԅᣒ
钢绞线尚无导波传播的解析解，端面和侧面传感器 सઢҧគѿૉಖ I stf 1.5
实测波形成分不得而知，实验中分别在端面和侧面 1.0
布置传感器分析传感器布置位置对应力识别结果 0.5
0
的影响。相同荷载工况、相同激励源输入条件下，端 0.2 0.3 0.4 0.5 0.6 0.7
面、侧面实测输出波形的识别指标 I stf 计算结果如 सઢҧ F m
图7所示。 图 8 加卸载时识别指标曲线
由图 7知，无论传感器布置在端面还是侧面，实 Fig. 8 Identification index curve for loading and
测数据计算的识别指标I stf 曲线表现出相同的单调 unloading process