Page 55 - 《应用声学》2020年第1期

第 39 卷 第 1 期 李帆等： 页岩可压裂性声学模型及应用 51

和断裂韧性对于页岩储层可压裂性的影响程度的 DY2 DY5 DY4-V ౐ඝവ᧚
58.0
相对重要性。 56.7
55.5
900 54.2
52.9
层次分析法将一个复杂问题转化为目标、准则 51.6
50.3
49.1
47.8
和方案等层次，然后进行定量和定性分析，通过对复 1200 46.5
45.2
44.0
杂本质和相关影响因素深入分析后，绘制清晰的层 ௑ᫎ/ms 1500 42.7
41.4
40.1
38.8
次结构图并进行判别预测。按照层次分析法递阶层 37.6
36.3
35.0
33.7
次原理，结合工区地质情况，确定岩石脆性和断裂 1800 32.5
31.2
29.9
28.6
韧性对于页岩储层可压裂性的影响程度的相对重 27.3
0 100 200 300 400 500 600 700
要性并给出标度，其判断准则按一定的标度进行设 CDP᥋ᬷ
(a) ԯҒुভԦ໦౐ඝവ᧚ᤌ̌Җ᭧
定 [19] 。
对 岩 石 脆 性、 断 裂 韧 性 进 行 标 度 赋 值 (如 DY2 DY5 DY4-V ෽౛උ
0.3506
表 1 所 示)， 并 构 造 判 断 矩 阵， 采 用 方 根 法 求 900 0.3447
0.3388
0.3329
0.3270
解判断矩阵的最大特征值所对应的特征向量为 1200 0.3211
0.3152
0.3093
(1.73205,0.57735)，对特征向量做归一化处理后得 ௑ᫎ/ms 0.3034
0.2975
0.2917
0.2799
到权重向量 C = (0.75, 0.25)。因此，页岩储层可压 1500 0.2858
0.2740
0.2681
0.2622
裂性影响因素岩石脆性、断裂韧性的权重系数分别 0.2563
0.2504
1800 0.2445
0.2386
是0.75和0.25，即C 1 = 0.75，C 2 = 0.25。 0.2327
0.2269
0.2210
0.2151
0.2092
表 1 页岩储层可压裂性评价判断矩阵因素赋值 0 100 200 300 400 500 600 700
CDP᥋ᬷ
Table 1 Assignment of judgement matrix (b) ԯҒुভԦ໦෽౛උᤌ̌Җ᭧
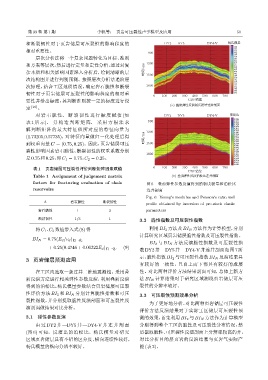
factors for fracturing evaluation of shale 图 6 叠前弹性参数反演得到的杨氏模量和泊松比
reservoirs 连井剖面
Fig. 6 Young’s modulus and Poisson’s ratio well
A 岩石脆性 断裂韧性
profile obtained by inversion of pre-stack elastic
岩石脆性 1 3 parameters
断裂韧性 1/3 1 3.2 脆性指数及可压裂性指数
将C 1 、C 2 数值带入式(8)得 利用 BI 2 方法及 BI N 方法作为计算模型，分别
计算研究区域页岩储层脆性指数及可压裂性指数。
BI N = 0.75(E d /ν d ) 归一化
BI 2 与 BI N 方法反演脆性指数及可压裂性指
+ 0.25(0.4746 + 0.00322E d ) 归一化 . (9) 数 DY2 井 —DY5 井 —DY4-V 井连井剖面如图 7 所
示，脆性指数 BI 2 与可压裂性指数 BI N 反演结果具
3 页岩储层预测应用
有较好的一致性，且自上而下都具有较好的成层
在工区内选取一条过井二维地震测线。采用叠 性。对比两种评价方法结果剖面可知，总体上新方
前反演方法进行相关弹性参数反演，利用叠前反演 法 BI N 计算结果对于研究区域测线页岩储层可压
得到的泊松比、杨氏模量参数结合页岩储层可压裂 裂性的分辨率较好。
性评价方法 BI 2 和 BI N 分别计算脆性指数和可压 3.3 可压裂性预测效果分析
裂性指数，并分别提取脆性反演剖面和可压裂性反
为了更好地分析、对比两种页岩储层可压裂性
演剖面做结果对比分析。
评价方法反演结果对于实际工区储层可压裂性预
3.1 弹性参数反演 测的效果，首先利用BI 2 与BI N 方法作为计算模型
由 过 DY2 井 —DY5 井 —DY4-V 井 连 井 剖 面 分别得到整个工区的脆性及可压裂性分布情况，然
(图 6) 可知，反演出的泊松比、杨氏模量对研究 后截取脆性、可压裂性反演剖面上分辨率较高的井，
区域页岩储层具有不错的区分度，横向连续性较好， 对比分析目的层页岩的反演结果与页岩气实际产
杨氏模量的纵向分辨率较好。 能(表2)。