Page 119 - 《应用声学》2020年第2期

第 39 卷 第 2 期 贾基东等： 一种基于随机序列的正交离散频率编码信号 277

方程组 [17] ： 所得到的时间序列就出现很大的变化。变量x(t) 的

采样序列在信号处理特性上优于 y(t) 和 z(t)，因此
 ˙x = −σ (x − y) ,


 在构造正交编码时通常采用x(t)的采样序列。
˙ y = −xz + rx − y, (4)

 2.2 Bernoulli混沌序列

 ˙ z = xy − bz.
Bernoulli 混沌是一种离散时间混沌系统，可描
当式 (4) 中 3 个参数 σ、r、b 满足如式 (5) 时，
述为如式(6)的更新方程 [16] ：
Lorenz系统会出现混沌解。 
  bx k + a, x k < 0,
 σ > b + 1, (6)
 x k+1 =
(5)  bx k − a, x k > 0,
σ (σ + b + 3)

 r > .
σ − b − 1 其中，a、b为混沌映射参数，a = 0.5, b = 2−ε，ε为一
采用四阶龙格库塔法求解 Lorenz方程组，设定 接近于 0 的极小正值。x k ∈ [−0.5, 0.5) 为过程变量，
采样率为 2000 Hz，可得到 3 个状态变量 x(t)、y(t)、 b 值越接近 2，混沌序列值在混沌吸引域 [−0.5, 0.5)
z(t) 的采样序列。图 2 是一个 Lorenz 系统的三维演 的遍历性越好，一组Bernoulli混沌序列如图4所示。
示图，其状态轨迹反复折叠形成一个类似蝴蝶的图 0.5
形，在 3 个维度上均有界，吸引子上也没有交叉点， 0.4
表现出整体混沌局部稳定的特点。图3 是Lorenz系 0.3
0.2
统3个状态变量的时间序列，3个序列均表现出非周
0.1
期性和对初值的敏感性，当初值出现很小的变化时 x↼k↽ 0
-0.1
-0.2
-0.3
4000
-0.4
3000
z -0.5
2000
0 200 400 600 800 1000
k
1000
0
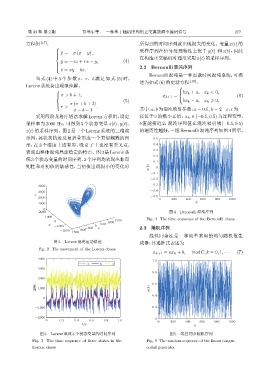
2000 图 4 Bernoulli 混沌序列
1000
0 1000 1500 Fig. 4 The time sequence of the Bernoulli chaos
y 500
-1000 -500 0 x 2.3 随机序列
-2000 -1000
-1500
线性同余法是一种简单常用的均匀随机数生
图 2 Lorenz 混沌运动轨迹 成器，其递推式表述为
Fig. 2 The movement of the Lorenz chaos
x k+1 = ax k + b, modC, k = 0, 1, · · · (7)
4000
⊲
x y z
3000
⊲
2000
⊲
گಖ 1000 x↼k↽

⊲
0
-1000 ⊲

-2000 
0 0.2 0.4 0.6 0.8 1.0
     
t/s
k
图 3 Lorenz 混沌 3 个状态变量的时间序列 图 5 线性同余随机序列
Fig. 3 The time sequence of three states in the Fig. 5 The random sequence of the linear congru-
Lorenz chaos ential generator