Page 21 - 《应用声学》2020年第3期

第 39 卷 第 3 期 余忠儒等： 基于近场辐射声压信号的索力识别方法 341

由图 4 可知在无噪声情况下，结构振动加速度 8.0
6.0
响应与近场辐射声压响应具有相同的趋势，与理 4.0
论推导相一致。在实际测试过程中，结构振动辐射 IMF1/Pa 2.0 0
声压信号往往会受到环境噪声干扰，为模拟信号受 -2.0
到噪声干扰的情况，现在对结构辐射声压信号添加 -4.0
-6.0
高斯白噪声，并基于 FFT 大致确定频率响应范围。 -8.0
0 0.3 0.5 0.8 1.0 1.3 1.5 1.8 2.0 2.3 2.5 2.8 3.0 3.3 3.5 3.8 4.0
对上述0.1 m 处近场处辐射声压信号添加信噪比为 ௑ᫎ/s
0.5 的高斯白噪声，并由 FFT 分析得到一阶频率响
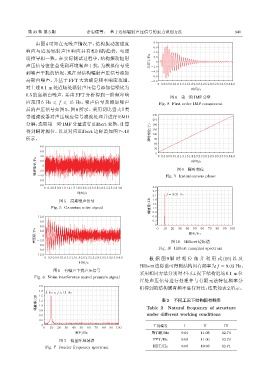
图 8 第一阶 IMF 分量
应范围 5 Hz 6 f 6 15 Hz，噪声信号及添加噪声 Fig. 8 First order IMF component
后的声压信号如图 5、图 6 所示。采用切比雪夫 I 类
带通滤波器对声压响应信号滤波处理并进行 EMD 240
210
分解，选取第一阶 IMF 分量进行 Hilbert 变换，计算 180
得到瞬时相位，以及对应 Hilbert 边际谱如图 7∼10 ᅯ௑ᄱͯ/(O) 150
120
所示。 90
60
8.0
30
6.0
0
4.0 0 0.3 0.5 0.8 1.0 1.3 1.5 1.8 2.0 2.3 2.5 2.8 3.0 3.3 3.5 3.8 4.0
٪ܦηՂ/Pa -2.0 0 图 9 瞬时相位
2.0
௑ᫎ/s
-4.0
-6.0 Fig. 9 Instantaneous phase
-8.0
0 0.3 0.5 0.8 1.0 1.3 1.5 1.8 2.0 2.3 2.5 2.8 3.0 3.3 3.5 3.8 4.0 3.0
2.7
௑ᫎ/s f/⊲ Hz
2.1
ࣨϙ៨/dB 1.5
图 5 高斯噪声信号 1.8
Fig. 5 Gaussian noise signal 1.2
0.6
12.0 0.9
9.0 0.3
0
6.0 0 10 20 30 40 50 60 70 80 90 100
ܦԍጟ/Pa -3.0 0 ᮠဋ/Hz
3.0
-6.0 图 10 Hilbert 边际谱
Fig. 10 Hilbert marginal spectrum
-9.0
-12.0
根 据 图 9 瞬 时 相 位 角 并 利 用 式 (16) 以 及
0 0.3 0.5 0.8 1.0 1.3 1.5 1.8 2.0 2.3 2.5 2.8 3.0 3.3 3.5 3.8 4.0
௑ᫎ/s
Hilbert边际谱可得到结构固有频率为f = 9.03 Hz。
图 6 有噪声干扰声压信号
采用相同方法分别对不同工况下结构近场 0.1 m 位
Fig. 6 Noise interference sound pressure signal
置处声压信号进行处理并与有限元法特征频率分
2.0
析得到的结构固有频率进行对比，结果如表2所示。
1.8
 Hz Ĺ f Ĺ  Hz
1.5
ࣨϙ៨/dB 1.3 Table 2 表 2 Natural frequency of structure
不同工况下结构固有频率
1.0
0.8
under different working conditions
0.5
0.3
0 工况编号 I II III
0 10 20 30 40 50 60 70 80 90 100
ᮠဋ/Hz 数值解/Hz 9.01 11.03 12.74
图 7 傅里叶频域谱 FFT/Hz 9.03 11.00 12.70
Fig. 7 Fourier frequency spectrum HHT/Hz 9.03 10.98 12.71