Page 44 - 《应用声学》2020年第3期

364 2020 年 5 月

Ѻ൓҂᣺ ቫ᭧ڀฉ Ѻ൓҂᣺ Ꭵᬞڀฉ ቫ᭧ڀฉ
0.4 0.4
0.2 0.2
ᄱࠫࣨϙ 0 ᄱࠫࣨϙ 0

-0.2 -0.2

-0.4 -0.4

0 5 10 15 20 25 30 0 5 10 15 20 25 30
௑ᫎ/µs ௑ᫎ/µs
(b) 0.5 mmᎥᬞଌஆηՂ
(a) ௄ᎥᬞଌஆηՂ
Ѻ൓҂᣺ Ꭵᬞڀฉ ቫ᭧ڀฉ Ѻ൓҂᣺ Ꭵᬞڀฉ ቫ᭧ڀฉ
0.4 0.4

0.2 0.2
ᄱࠫࣨϙ 0 ᄱࠫࣨϙ 0

-0.2 -0.2
-0.4 -0.4

0 5 10 15 20 25 30 0 5 10 15 20 25 30
௑ᫎ/µs ௑ᫎ/µs
(c) 1.0 mmᎥᬞଌஆηՂ (d) 1.5 mmᎥᬞଌஆηՂ

Ѻ൓҂᣺ Ꭵᬞڀฉ ቫ᭧ڀฉ Ѻ൓҂᣺ Ꭵᬞڀฉ ቫ᭧ڀฉ
0.4 0.4

0.2 0.2
ᄱࠫࣨϙ 0 ᄱࠫࣨϙ 0

-0.2 -0.2
-0.4 -0.4

0 5 10 15 20 25 30 0 5 10 15 20 25 30
௑ᫎ/µs ௑ᫎ/µs
(e) 2.0 mmᎥᬞଌஆηՂ (f) 2.5 mmᎥᬞଌஆηՂ
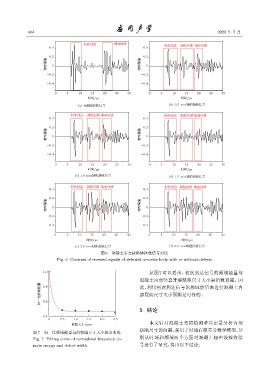
图 6 混凝土有无缺陷体接收信号对比
Fig. 6 Contrast of received signals of defected concrete body with or without defects

从图 7 可以看出，初次到达信号的频域能量与
1.0
混凝土内部竖直开裂缺陷尺寸大小呈指数衰减。因
ॆʷӑᮠ۫ᑟ᧚ 0.8 此，利用初次到达信号的频域能量来进行混凝土内

部裂纹尺寸大小预测是可行的。
0.6
5 结论
0.4
0 0.5 1.0 1.5 2.0 2.5
本文针对混凝土无损检测难以定量分析内部
Ꭵᬞܸ࠵/mm
缺陷尺寸的问题，采用了时域有限差分数学模型，分
图 7 归一化频域能量与的缺陷尺寸大小拟合曲线
Fig. 7 Fitting curve of normalized frequency do- 别从时域和频域两个方面对混凝土超声波接收信
main energy and defect width 号进行了研究，得出以下结论：