Page 43 - 《应用声学》2020年第3期

第 39 卷 第 3 期 刘昌明等： 时域有限差分法的混凝土超声波损伤分析 363

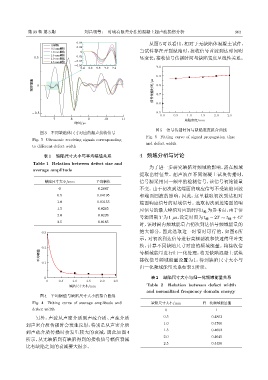
0.04 从图 5 可以看出，相对于无缺陷体混凝土试件，
௄Ꭵᬞ
0.5 mmᎥᬞ 0.02
1.0 mmᎥᬞ 0 当试件存在开裂缺陷时，接收信号首波到达时间明
1.5 mmᎥᬞ
0.5 -0.02 显变长，接收信号传播时间与缺陷宽度呈线性关系。
2.0 mmᎥᬞ
2.5 mmᎥᬞ -0.04
-0.06
6.4 6.6 6.8 7.0 7.2 7.0
6.9
ᄱࠫࣨϙ 0 ηՂ͜୧௑ᫎ/µs 6.8

6.7
6.6

-0.5 6.5
0.0 0.5 1.0 1.5 2.0 2.5
7 8 9 10 11
Ꭵᬞࠕए/mm
௑ᫎ/µs
图 5 信号传播时间与缺陷宽度拟合曲线
图 3 不同缺陷体尺寸对应的超声接收信号
Fig. 5 Fitting curve of signal propagation time
Fig. 3 Ultrasonic receiving signals corresponding
and defect width
to different defect width
表 1 缺陷尺寸大小与平均幅值关系 4 频域分析与讨论
Table 1 Relation between defect size and
为了进一步研究缺陷对频域的影响，需在频域
average amplitude
提取出特征量。超声波在不同混凝土试块传播时，
缺陷尺寸大小/mm 平均幅值 信号源采用同一频率的检测信号，该信号初始能量
0 0.2847 不变。由于初次到达端面的响应信号不受缺陷回波
0.5 0.04195 和端面回波的影响，因此，这里截取初次到达相对
1.0 0.03155 端面响应信号的时域信号。选取初次到达端面的响
1.5 0.0265
应信号的最大峰值对应的时间t 为参考点，由于信
峰
2.0 0.0226
号源周期T 为1 µs，设定时窗为t − 2T ∼ t + 4T
峰
峰
2.5 0.0185
时，该时窗内频域能量占初次到达信号频域能量的
绝大部分，因此选取这一时窗时可行的，如图 6 所
0.3
示。对初次到达信号进行高频滤波和快速傅里叶变
换，计算不同缺陷尺寸对应的频域能量。将接收信
0.2
ࣱکࣨϙ 号频域能量进行归一化处理，将无缺陷混凝土试块
0.1 接收信号频域能量设置为 1，得到缺陷尺寸大小与
归一化频域能量关系如表2所示。

0 表 2 缺陷尺寸大小与归一化频域能量关系
0 0.5 1.0 1.5 2.0 2.5
Table 2 Relation between defect width
Ꭵᬞࡇܸࠪ࠵/mm
and normalized frequency domain energy
图 4 平均幅值与缺陷尺寸大小的拟合曲线
Fig. 4 Fitting curve of average amplitude and 缺陷尺寸大小/mm 归一化频域能量值
defect width 0 1
另外，声波从声密介质到声疏介质、声疏介质 0.5 0.4803
到声密介质传播时会发生反射，特别是从声密介质 1.0 0.4760
1.5 0.4692
到声疏介质传播时会发生较大的衰减，因此如图 4
2.0 0.4645
所示，从无缺陷到有缺陷得到的接收信号幅值衰减
2.5 0.4490
比有缺陷之间的衰减要大很多。