Page 42 - 《应用声学》2020年第3期

362 2020 年 5 月

式 (4) 中：变量下标表示空间位置，上标表示时刻；
其中， 3 时域分析与讨论
( )
f n = α 1 σ n − σ n 超声波衰减公式为
σ xx xx i+1/2,k−1/2 xx i−1/2,k−1/2
i,k−1/2
( ) −αa 0
+ α 2 σ n −σ n , p = p 0 e , (5)
xx i+3/2,k−1/2 xx i−3/2,k−1/2
( ) 其中，p 0 为起始声压，p 为距声源 a 0 处声压，α 为介
n n n
g = α 1 σ − σ
σ xz xz i,k xz i,k−1
i,k−1/2 质衰减系数，a 0 为超声发射器与接收器之间的尺
( )
+ α 2 σ n − σ n , 寸，且 a 0 为超声发射器与接收器之间密实体尺寸
xz i,k+1 xzx i,k−2
α 1 = 1.125, α 2 = 0.04167. a 密实体 与缺陷体尺寸a 缺陷体 之和。
介质衰减系数 α 的尺度大小与材料性质、超声
边界条件采用 Clayton-Engguist-MaJda2 阶吸收边
波频率有关。频率一定时，超声波在混凝土内部的
界条件 [17] 。
密实体介质衰减系数 α 与缺陷体介质衰减系
时域有限差分法利用近似的差分方程和上一 密实体
数α 是确定值。当混凝土内部存在不密实缺陷
时刻的波场值，计算出下一时刻的波场值，随着时间 缺陷体
体时，由于介质衰减系数 α 的值远大于 α ，
递推时，便能获得各质点处各时刻的波场值。 缺陷体 混凝土
超声信号衰减主要受介质衰减系数较大的 α 缺陷体
2 混凝土试件结构及测试装置布置 对应缺陷体尺寸a 缺陷体 的影响。
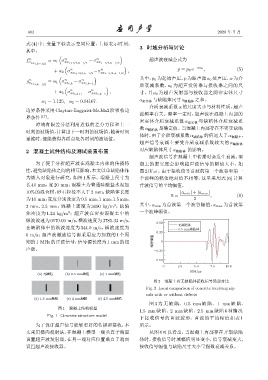
超声波信号在混凝土中传播时会发生衰减，混
为了便于分析超声波在混凝土内部的传播特 凝土的密实度会影响超声波信号的幅值大小，如
性，避免缺陷体之间的相互影响，本文以单缺陷体作 图 2 所示。由于接收信号首波的第一个波谷和第一
为嵌入对象进行研究，如图 1 所示。混凝土尺寸为 个波峰的幅值绝对值不相等，这里采用式 (6) 计算
长 40 mm，宽 20 mm；混凝土为普通硅酸盐水泥加 首波信号的平均幅值，
10% 的混合材，砂石粒径不大于 2 mm；缺陷体长度 |a min | + |a max |
a = , (6)
为10 mm，宽度分别设定为0.5 mm、1 mm、1.5 mm、 2
2 mm、2.5 mm；混凝土密度为 3000 kg/m ，缺陷 其中，a min 为首波第一个波谷幅值，a max 为首波第
3
3
体密度为 1.24 kg/m ；超声波在密实混凝土中的 一个波峰幅值。
纵波波速为 6170.09 m/s，横波速度为 3785.33 m/s，
0.50
在缺陷体中的纵波速度为 344.0 m/s，横波速度为 ௄Ꭵᬞʹ
0.5 mmᎥᬞʹ
0.25
0 m/s；超声波激励信号源采用应力加载的 1 个周
期的 1 MHz 的正弦信号，信号源长度为 1 mm 的线 ᄱࠫࣨϙ 0
声源。 -0.25

-0.50
0 2.5 5.0 7.5 10.0
௑ᫎ/µs
(a) ௄Ꭵᬞ (b) 0.5 mmᎥᬞ (c) 1 mmᎥᬞ
图 2 混凝土有无缺陷体接收信号局部对比
Fig. 2 Local comparison of concrete receiving sig-
nals with or without defects
(d) 1.5 mmᎥᬞ (e) 2 mmᎥᬞ (f) 2.5 mmᎥᬞ
图 3 为 无 缺 陷、 0.5 mm 缺 陷、 1 mm 缺 陷、
图 1 混凝土结构模型
1.5 mm 缺陷、2 mm 缺陷、2.5 mm 缺陷 6 种情况
Fig. 1 Concrete structure model
下接收信号的首波波形，首波的平均幅值如表 1
为了保证超声信号能够更好的传播和接收，本 所示。
文采用横向投射法，在混凝土模型一端垂直于端面 从图 4 可以看出，当混凝土内部存在开裂缺陷
设置超声波发射器，在另一端对应位置垂直于端面 体时，接收信号时域幅值明显变小，信号衰减变大，
设置超声波接收器。 接收信号幅值与缺陷尺寸大小呈指数衰减关系。