Page 38 - 《应用声学》2020年第3期

358 2020 年 5 月

此外需要指出的是，当线阵进行稀疏处理后主 简单等特点，但是在收敛性方面还略有不足，在多
瓣窄、旁瓣高，当稀疏阵列降低至 14 个以及 11 个阵 约束条件下求解问题上容易出现局部最优解的问
元时，如图 10、图 11 及图 12 所示，稀疏阵列虽然在 题，可能在最终迭代结束后得不到最优解，这可以通
全聚焦成像上能够实现所需的检测及成像效果，但 过算法的进一步优化或使用混合优化算法 (如粒子
能否进行普通相控线扫和扇扫检测需要通过对不 群-遗传) 来解决。另一方面，虽然目前粒子群算法、
同类型缺陷试块进行验证。与此同时，随着移动处 模拟退火算法、差分进化算法等优化算法在阵列稀
理器和 5G 技术的高速发展，目前先进的相控阵超 疏和阵元布置方面存在较多的理论成果，但在超声
声检测产品已能实现实时的 B 扫成像，因此普通扫 检测领域，特别是在超声相控阵的快速成像、相控
查的速度优化已不是研究重点。因此，快速线扫、扇 阵稀疏阵列的适应度函数设计、非均匀阵列孔径补
扫与高效率稀疏阵列相控阵全聚焦成像相结合的 偿等方面的研究和应用仍然较为薄弱。
复合扫查将是未来的研究方向之一。 此外，在实际应用中，还需要考虑各向异性材
料、试块表面质量、近场缺陷和不同种类缺陷识别
35
11ጸҫిሪႠ᫼Ћ᫼ѵ 的问题，这也是稀疏相控阵进行实际检测和后处理
30 14ጸҫిሪႠ᫼Ћ᫼ѵ
ಖю32᫼Ћ᫼ѵ 成像时需要考虑的因素。
25
ᣣ࠱ूए/dB 20 -5 0 11᫼ЋሪႠጳ᫼

ಖю32کӉጳ᫼
15
-10
10
ᣣ࠱ूए/dB -20
5 -15
0
-80 -60 -40 -20 0 20 40 60 80 -25
ᝈए/(O)
-30
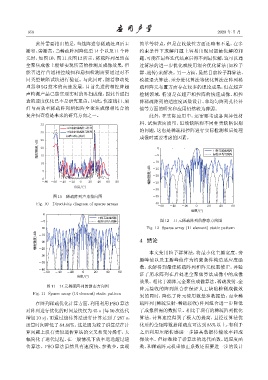
图 10 稀疏阵列声束指向图 -35
Fig. 10 Directivity diagram of sparse arrays -40
-60 -40 -20 0 20 40 60
ᝈए/(O)
0
14᫼ЋሪႠጳ᫼
-5 ಖю32کӉጳ᫼ 图 12 11 元稀疏阵列的静态方向图
-10 Fig. 12 Sparse array (11 element) static pattern
ᣣ࠱ूए/dB -15 4 结论

-20
-25
本文使用粒子群算法，将最小化主瓣宽度、旁
-30
瓣峰值以及主瓣峰值作为约束条件构造适应度函
-35
数，求解得到最佳稀疏阵列和阵元权重修正，并验
-40
-60 -40 -20 0 20 40 60
证了所求阵列在后处理全聚焦算法成像中的成像
ᝈए/(O)
效果。相比于满阵元全聚焦成像算法，稀疏发射-全
图 11 14 元稀疏阵列的静态方向图
阵元接收的阵列组合在保证人工缺陷检测成像效
Fig. 11 Sparse array (14 element) static pattern
果的同时，降低了阵元使用数量和数据量，而全稀
在阵列稀疏优化计算方面，利用利用PSO算法 疏阵列 (稀疏发射 -稀疏接收) 阵列组合进一步降低
对阵列进行优化的时间最快仅为45 s (每50次迭代 了成像所需的数据量。相比于现有的稀疏阵列优化
增加 10 s)，而通过遗传算法进行计算达到了 287 s， 算法，计算速度得到了极大的提高，且经过算法优
运算时间降低了84.86%。这是因为粒子群算法在计 化后的全矩阵数据稀疏度可达到 85% 以上，有利于
算问题上没有类似遗传算法的交叉和变异操作，大 之后利用压缩传感进一步提高数据传输效率和成
幅简化了迭代过程，在一般情况下效率远远超过遗 像效率。但标准粒子群算法的迭代函数、适应度函
传算法。PSO 算法虽然具有速度快、参数少、实现 数、和稀疏阵元权重修正系数还需要进一步的设计