Page 118 - 《应用声学》2020年第4期

604 2020 年 7 月

v s=10 m/s 表 5 关联维数与系统动力学特性
1.0 v s=15 m/s
v s=20 m/s Table 5 The relationship of correlation
v s=25 m/s
dimension and system dynamic character-
0.5
R↼τ↽ 1/e 23 36 47 72 istic
0 关联维数取值 动力学特性 关联维数取值 动力学特性
0 定常运动 1 周期振动
-0.5
0 2 0 4 0 6 0 8 0 1 0 0 2 或 3 准周期振动 无穷大 随机运动
τ 正分数 混沌运动
(a) ˀՏѭҐᤴए
因此，根据计算得到无氧铜在不同切削参数下
a p =10 mm
1.0 a p =20 mm 的声发射信号关联维数 D，利用表 5 可进一步确定
a p =30 mm 该声发射信号系统属于何种运动状态特性。
a p =40 mm
0.5 27 62 3.3.1 切削速度对关联维数的影响分析
R↼τ↽ 1/e 21 48
切削速度对声发射信号双对数曲线数的影响
0
如图 7 所示。随着嵌入维数的增大，双对数曲线的
lnC(r) 取值逐渐增大，不同切削速度的双对数曲线
-0.5
0 2 0 4 0 6 0 8 0 1 0 0 变化特征较为相似，不同切削速度的双对数曲线均
τ
(b) ˀՏѭҐງए 呈阶段性增长趋势，并逐渐收敛于饱和状态。当 m
较小时，曲线斜率较小；随着 m 的增大，曲线斜率
v w =10 m/min
1.0 v w =15 m/min 亦随之逐渐增大，分形区域无标度区间不断缩小并
v w=20 m/min 趋于饱和；在 D 值达到饱和之后，随着 m 的增加，
v w =25 m/min
0.5 26 47 ln C(r) 值基本不再发生变化。另外，在切削速度较
R↼τ↽ 1/e 23 38 小时 (v s = 10 m/s，图 7(a))，ln C(r) 的取值范围在

0 −1.1 ∼ 0之间，随着切削速度的增大，其他3 个切削
速度 (图 7(b)、7(c) 和 7(d)) 的 lnC(r) 的取值范围则
-0.5 扩大到−7.9 ∼ 0之间。通过对无标度区间的斜率计
0 2 0 4 0 6 0 8 0 1 0 0
τ
算，可得切削速度与关联维数的关系。
(c) ˀՏᤉፌᤴए
切削速度对关联维数的影响关系见图 8(a)，不
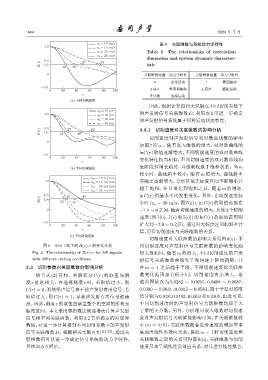
图 6 不同工况下的 R(τ)-τ 的变化关系 同切削速度对声发射信号关联维数的影响变化趋
Fig. 6 The relationship of R(τ)-τ for AE signals 势大致相同，随着 m 的增大，不同切削速度的声发
with different cutting conditions 射信号关联维数曲线先呈现快速下降的趋势，并
3.3 切削参数对关联维数的影响分析 在 m = 4 之后趋于平缓。不同切削速度的关联维

结合式 (2) 可知，关联积分 C(r) 的取值与测 数变化范围是有所不同，切削速度由小增大，取
度 r 息息相关，在选择测度 r 时，若取值过小，则 值范围依次为 0.0282 ∼ 0.0656、0.0488 ∼ 0.0687、
C(r) = 0，系统噪声信号将干扰声发射有用信号；若 0.0389 ∼ 0.0631、0.0303 ∼ 0.0583，趋于平稳时的取
取值过大，则 C(r) = 1，导致声发射有用信号被淹 值分别为0.028、0.0493、0.0393和0.0305，由此可见，
没。因此，测度r 的取值应涵盖整个相空间的所有无 不同切削速度时的声发射信号关联维数均属于大
标度区间。本文采用等指数比例递增法计算声发射 于零的正分数。另外，分析相同嵌入维数时切削速
信号相空间关联函数。利用 3.2 节所确定的时延参 度对声发射信号关联维数影响可知，在关联维数较
数值，可进一步计算得到不同切削参数下的声发射 小 (m = 1) 时，关联维数随着进给速度的增加基本
信号关联维数 D。根据相关文献可知 [19,21] ，通过关 呈现出线性负效应关系，提取 m = 1 时切削速度和
联维数值可以进一步确定信号系统的动力学特性， 关联维数之间的关系可得图 8(b)，关联维数与切削
具体如表5所示。 速度基本呈现线性负效应关系，对其进行线性拟合，