Page 122 - 《应用声学》2020年第4期

608 2020 年 7 月

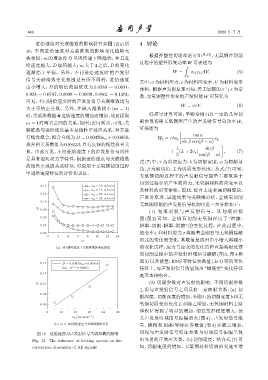
进给速度对关联维数的影响特性如图 12(a) 所 4 讨论
示，不同进给速度对关联维数的影响变化趋势大
根据弹塑性切削理论可知 [5,13] ，无氧铜在切削
致相似，m 的增加使 D 呈现快速下降趋势，并且进
过程中的塑性形变功率W 可表述为
给速度越大，D 取值越大；m 大于 4 之后，D 的变化 ∫
逐渐趋于平稳。另外，不同进给速度时的声发射 W = σ ij ε ij dV, (5)
V
信号关联维数变化范围是有所不同的，进给速度
其中，σ 为材料应力，ε为材料应变率，V 为材料变形
由小增大，D 的取值范围依次为 0.0389 ∼ 0.0631、
体积。根据声发射原理可知，若无氧铜的σ 与ε为常
0.024 ∼ 0.0747、0.0698 ∼ 0.0939、0.0861 ∼ 0.1361，
数，无氧铜塑性形变的声发射能W 可简化为
可见，不同进给速度时的声发射信号关联维数均为
W = σεV. (6)
大于零的正分数。另外，在嵌入维数较小 (m = 1)
时，关联维数随着进给速度的增加而增加，故而提取 经推导计算可知，单颗金刚石以一定的几何切
m = 1时两者之间的关系，如图12(b)所示，可见，关 削参数切削无氧铜所产生的声发射信号总功率 W t
联维数与进给速度基本呈线性正效应关系，对其进 可描述为
[
cos α
行线性拟合，拟合直线为D = 0.00476v w + 0.00858， W t = τbv s a p
sin β cos(β − α)
拟合相关系数值为0.88033，具有良好的线性拟合关 ]
1 sin β
系。由此可见，不同进给速度下的声发射信号同样 + (L + 2v s ) , (7)
3 cos(β − α)
是具有混沌动力学特性，根据进给速度与关联维数
式 (7) 中，τ 为剪切应力，b 为切削宽度，α 为切削前
的线性正效应关系特征，可应用于无氧铜切削过程
角，β 为剪切角，L 为切屑变形长度。从式 (7) 可知，
中进给速度特征的评价和表征。
无氧铜切削过程中的声发射信号能量主要取决于
切削过程中所产生的应力、无氧铜材料的应变率以
0.14 v w=10 m/min
v w=15 m/min 及材料的形变体积。因此，综合上述金属切削理论、
0.12 v w=20 m/min
v w=25 m/min 声发射原理、试验结果与关联维分析，金刚石切削
0.10
无氧铜切削的声发射信号机制可进一步分析如下：
D 0.08
(1) 划痕形貌与声发射信号。 从划痕形貌
0.06
图 (图 2) 可知，金刚石切削无氧铜经历了 “滑擦 -
0.04 耕犁 -切削 -耕犁 -滑擦” 的变化过程，在此过程中，
0.02 应变率ε 和材料应力σ 将随着金刚石与无氧铜接触
0 2 4 6 8 10 12 14
形式的变化而变化，其数值呈现出由小增大再减小
m
(a) ˀՏᤉፌᤴएʾТᐏ፥஝ᄊԫӑৱц 的变化历程，应力与应变的变化历程直接映射反馈
到切削过程中的声发射时域信号振幅 (图 3、图 4 和
图5) 以及能量、RMS 等特征参数值 (表 4) 等的变化
0.14 D=0.00476v w +0.00858
Adj. R =0.88033 特征上，与声发射信号所呈现出 “橄榄型” 变化特征
2
0.12
是基本相吻合。
(2) 切削参数对声发射的影响。不同切削参数
D 0.10
工况与声发射信号之间具有一定映射关系：(a) 切
0.08
削深度。切削深度的增加，金刚石的切削宽度b和无
0.06 氧铜切屑变形长度 L 亦随之增加，无氧铜材料去除
体积 V 得到了明显的增加，塑性变形程度增大，使
8 1 2 1 6 2 0 2 4 2 8
v w /(mSmin -1 ) 其声发射时域信号振幅增大 (图 4)，声发射信号能
(b) m=1௑ᤉፌᤴएˁТᐏ፥஝ᄊТጇ 量、振幅和 RMS 等特征参数值 (表 4) 亦随之增加，

图 12 进给速度对声发射信号关联维数的影响 切深与声发射信号特征参数与时域信号振幅呈现
Fig. 12 The influence of feeding speeds on the 出显著的正效应关系。(b) 切削速度。结合式 (7) 可
correlation dimension of AE signals 知，切削速度的增加，无氧铜材料切屑形变速率增