Page 31 - 《应用声学》2020年第5期

第 39 卷 第 5 期 张雪冬等： 斜坡海底波导中随机声源的信道盲解卷积 673

4 -30
-20
2
-10
ࣨए 0 ᝈए/(°) 0
10
-2
20
-4 30
0 1 2 3 4 -20 -15 -10 -5 0
௑ᫎ/s ᑟ᧚/dB
(a) ଌஆηՂ (b) ฉౌڏ
ᑟ᧚/dB ᑟ᧚/dB
510 -10 510 -10

520 -20 520 -20
ງए/m ງए/m

530 -30 530 -30

540 -40 540 -40
1.00 1.02 1.04 1.70 1.72 1.74 1.76
௑ᫎ/s ௑ᫎ/s
(c) RBD-CIR (d) CIR

VLA
-θ
O
+θ

(e) ҂᣺ᝈθᄊگಖ

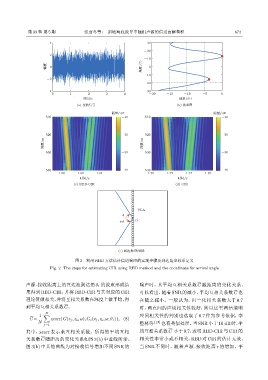
图 2 利用 RBD 方法估计信道响应的实现步骤及到达角坐标系定义
Fig. 2 The steps for estimating CIR using RBD method and the coordinate for arrival angle

声源 -接收距离上的直达波到达角 θ 1 的波束形成结 噪声时，其平均互相关系数 C 随距离的变化关系。
果得到 RBD-CIR，并将 RBD-CIR 与其对应的 CIR 可以看出，随着 SNR 的减小，平均互相关系数 C 也
理论值做相关，并将互相关系数在深度上做平均，得 在随之减小。一般认为，归一化相关系数大于 0.7
到平均互相关系数C， 时，两点间的声场相关性较好，所以这里两信道响
N
1 ∑ 应间相关性的判别也选取了 0.7 作为参考依据，李
C = xcorr{G(z j , z s , ω), G e (z j , z s , ω; θ 1 )}, (8)
N 整林等 [13] 也有类似处理。当SNR小于10 dB时，平
j=1
其中，xcorr 表示求互相关系数。所得的平均互相 均互相关系数C 小于0.7，表明RBD-CIR与CIR的
关系数 C 随距离的变化关系如图 3(b) 中蓝线所示。 相关性非常小或不相关，RBD 对 CIR 的估计无效。
图 3(b) 中其他曲线为对接收信号增加不同 SNR 的 当 SNR 不同时，随着声源 -接收距离 r 的增加，平