Page 34 - 《应用声学》2020年第5期

676 2020 年 9 月

ᑟ᧚/dB ᑟ᧚/dB ᑟ᧚/dB
1.0 0 1.0 0 1.0 0
1.5 -5 1.5 -5 1.5 -5
ᡰሏ/km 2.0 -10 ᡰሏ/km 2.0 -10 ᡰሏ/km 2.0 -10
2.5
2.5
2.5
-15 -15 -15
3.0 3.0 3.0
3.5 -20 3.5 -20 3.5 -20
-20 0 20 40 -20 0 20 40 -20 0 20 40 60
ᝈए/(°) ᝈए/(°) ᝈए/(°)
(a) φ=-2° (b) φ=1° (c) φ=5°

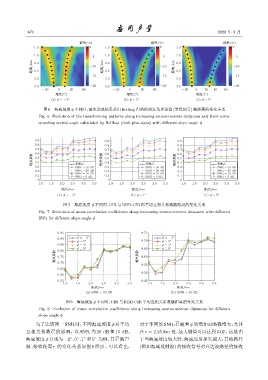
图 6 海底坡度 ϕ 不同时，波束形成结果及由 Bellhop 得到的到达角理论值 (黑色加号) 随距离的变化关系
Fig. 6 Evolution of the beamforming patterns along increasing source-receiver distances and their corre-
sponding arrival angle calculated by Bellhop (dark plus signs) with different slope angle ϕ

0.9 0.9 0.9
0.8 0.8 0.8
0.7 0.7 0.7
0.6 0.6 0.6
ᄱТጇ஝ 0.5 ᄱТጇ஝ 0.5 ᄱТጇ஝ 0.5
0.4
0.4
0.4
0.3 ௄٪ܦ 0.3 ௄٪ܦ 0.3 ௄٪ܦ
SNR=30 dB
SNR=30 dB
SNR=30 dB
0.2 SNR=20 dB 0.2 SNR=20 dB 0.2 SNR=20 dB
SNR=10 dB SNR=10 dB SNR=10 dB
0.1 SNR=0 dB 0.1 SNR=0 dB 0.1 SNR=0 dB
0 0 0
1.0 1.5 2.0 2.5 3.0 3.5 1.0 1.5 2.0 2.5 3.0 3.5 1.0 1.5 2.0 2.5 3.0 3.5
ᡰሏ/km ᡰሏ/km ᡰሏ/km
(a) φ=-2° (b) φ=1° (c) φ=5°
图 7 海底坡度 ϕ 不同时，CIR 与 RBD-CIR 的平均互相关系数随距离的变化关系
Fig. 7 Evolution of mean correlation coefficients along increasing source-receiver distances with different
SNR for different slope angle ϕ

0.95 0.75
0.90 φ=-2O φ=-2O
φ=0O 0.70 φ=0O
0.85 φ=1O φ=1O
φ=5O 0.65 φ=5O
0.80
ᄱТጇ஝ 0.75 ᄱТጇ஝ 0.60
0.70
0.55
0.65
0.50
0.60
0.55 0.45
1.0 1.5 2.0 2.5 3.0 3.5 1.0 1.5 2.0 2.5 3.0 3.5
ᡰሏ/km ᡰሏ/km
(a) SNR=20 dB (b) SNR=10 dB

图 8 海底坡度 ϕ 不同时，CIR 与 RBD-CIR 平均互相关系数随距离的变化关系
Fig. 8 Evolution of mean correlation coefficients along increasing source-receiver distances for different
slope angle ϕ
为了比较同一 SNR时，不同海底坡度 ϕ对平均 对于不同的SNR，C 随着ϕ的增加而略微增大，尤其
互相关系数 C 的影响，以 SNR 为 20 dB 和 10 dB， 在r = 2.25 km 处，最大增值可以达到0.07。这是由
海底坡度ϕ分别为−2 、0 、1 和5 为例，其C 随声 于当海底坡度较大时，海底反射损失越大，其他路径
◦
◦
◦
◦
源 -接收距离 r 的变化关系如图 8 所示。可以看出， (例如海底反射波)的接收信号对直达波路径的接收