Page 32 - 《应用声学》2020年第5期

674 2020 年 9 月

均互相关系数 C 均逐渐增大，这意味着估计到的 变化；但海底反射波的到达角θ 2 随海底坡度的增加
RBD-CIR 越准确。这是由于随着声源 -接收距离 r 而增大，且由于海底反射损失的影响，其在 θ 2 处的
的增加，声源所发出的信号在接收阵上越接近平面 幅度随着坡度的增加 ϕ 而减小。对于半无限空间的
波，波束形成的结果越精确，从而估计的 RBD-CIR 海底，其海底反射损失 (Reflection loss, RL) [10] 可
越精确。 表示为

ᑟ᧚/dB ρ b c b − ρ w c w
1.0 0 cos θ b cos θ w
RL(θ) = 20 lg , (9)
ρ b c b
+ ρ w c w
1.5 cos θ b cos θ w
-5
其中，c w 、ρ w 、θ w 和 θ b 分别表示在接近海底处海水
2.0
ᡰሏ/km -10 的声速、密度，声线入射角和透射角。透射角和入射
2.5
角的关系根据Snell定律 [10] 得到
-15 ( )
3.0 ω ω
+ iα b sin θ b = sin θ w . (10)
c b c w
3.5 -20
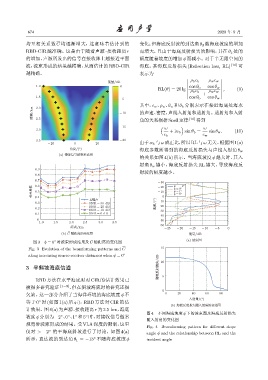
-20 0 20 由于α b 与ω 成正比，所以RL与ω 无关。根据图1(a)
ᝈए/(°)
海底参数所得到的海底反射损失与声线入射角 θ w
(a) ଌஆηՂฉౌॎੇڏ
的关系如图 4(b) 所示。当海底坡度 ϕ 越大时，其入
射角 θ w 越小，海底反射损失 RL 越大，导致海底反
0.9
射波的幅度越小。
0.8
0.7
-30 φ=-2O
0.6
⴨ޣ㌫ᮠ 0.5 -10 φ=0O
-20
φ=1O
φ=5O
0.4
௄٪ܦ 0
0.3 SNR=30 dB ᝈए/(°) 10
SNR=20 dB 20
0.2
SNR=10 dB 30
0.1 SNR=0 dB
40
0 50
1.0 1.5 2.0 2.5 3.0 3.5
60
ᡰሏ/km -25 -20 -15 -10 -5 0
-
(b) C ᬤᡰሏᄊԫӑڏ ᑟ᧚/dB
图 3 ϕ = 0 时波束形成结果及 C 随距离的变化图 (a) ฉౌڏ
◦
Fig. 3 Evolution of the beamforming patterns and C 15
along increasing source-receiver distances when ϕ = 0 ◦
3 平斜坡海底信道 ๒अԦ࠱૯ܿ/dB 10
RBD 方法在水平海底时对 CIR 的估计效果已 5
被很多研究验证 [1−9] ，但在斜坡海底时的研究还很
0
欠缺。这一部分介绍了当海洋环境的海底坡度 ϕ不 0 20 40 60 80
К࠱ᝈ/(°)
等于 0 时 (如图 1(a) 所示)，RBD 方法对 CIR 的估
◦
(b) ๒अԦ࠱૯ܿᬤК࠱ᝈᄊԫӑڏ
计效果。图4(a) 为声源 -接收距离 r 为2.5 km，海底
图 4 不同海底坡度 ϕ 下的波束图及海底反射损失
坡度 ϕ 分别为 −2 、0 、1 和 5 时，对接收信号做常
◦
◦
◦
◦
随入射角的变化图
规宽带波束形成的结果。受VLA 深度的限制，这里
Fig. 4 Beamforming pattern for different slope
仅对 > −2 的平海底斜坡进行了讨论。如图 4(a) angle ϕ and the relationship between RL and the
◦
◦
所示，直达波的到达角 θ 1 = −13 不随海底坡度 ϕ incident angle