Page 37 - 《应用声学》2020年第5期

第 39 卷 第 5 期 张雪冬等： 斜坡海底波导中随机声源的信道盲解卷积 679

ᑟ᧚/dB ᑟ᧚/dB
540 -10 510 -10

550 -20 520 -20
ງए/m ງए/m

560 -30 530 -30

-40 -40
570 540
1.8 2.0 2.2 0.7 0.8 0.9 1.0 1.1
௑ᫎ/s ௑ᫎ/s
(a) ଌஆງए540~570 mᄊCIR (b) ଌஆງए540~570 mᄊRBD-CIR

ᑟ᧚/dB ᑟ᧚/dB
540 -10 570 -10

550 -20 580 -20
ງए/m ງए/m

560 -30 590 -30

-40 -40
570 600
1.8 2.0 2.2 0.7 0.8 0.9 1.0 1.1
௑ᫎ/s ௑ᫎ/s
(c) ଌஆງए570~600 mᄊCIR (d) ଌஆງए570~600 mᄊRBD-CIR

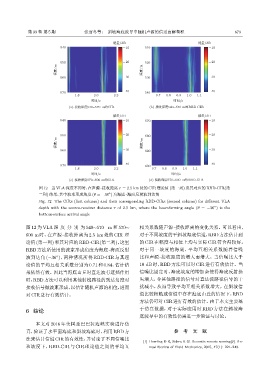
图 12 当 VLA 深度不同时，在声源 -接收距离 r = 2.5 km 处的 CIR 理论值 (第一列) 及其对应的 RBD-CIR(第
二列) 结果，其中波束形成角度 (θ = −36 ) 为海底 -海面反射波到达角
◦
Fig. 12 The CIRs (first column) and their corresponding RBD-CIRs (second column) for different VLA
depth with the source-receiver distance r of 2.5 km, where the beamforming angle (θ = −36 ) is the
◦
bottom-surface arrival angle

图 12 为 VLA 深 度 分 别 为 540∼570 m 和 570∼ 相关系数随声源 -接收距离的变化关系。可以看出，
600 m 时，在声源 -接收距离为 2.5 km 处的 CIR 理 对于不同坡度的平斜坡海底信道，RBD方法估计到
论值 (第一列) 和其对应的RBD-CIR(第二列)，这里 的 CIR 在幅度与相位上均与实际 CIR 符合得较好。
RBD方法所使用的波束形成角度为海底 -海面反射 对于同一坡度的海底，平均互相关系数随着信噪

波到达角 (−36 )，两种情况所得 RBD-CIR 与其理 比和声源 -接收距离的增大而增大。当信噪比大于
◦
论值的平均互相关系数分别为 0.71 和 0.84，估计结 10 dB 时，RBD 方法可以对 CIR 进行有效估计。当
果依然有效。因此当海底山丘对直达波有遮挡作用 信噪比固定时，海底坡度的增加会使得海底反射损
时，RBD方法可以利用其他射线路径的到达角度对 失增大，令其他路径的信号对直达波路径信号的干
接收信号做波束形成，以估计随机声源的相位，进而 扰减小，从而导致平均互相关系数增大。在斜坡信
对CIR进行有效估计。 道比较粗糙或信道中存在海底山丘的情况下，RBD
方法仍可对 CIR进行有效的估计。由于本文主要基
6 结论 于仿真数据，对于实际应用时 RBD 方法在斜坡海
底波导中的有效性仍需进一步验证与讨论。
本文对 2016 年美国圣巴巴拉海峡实验进行仿
真，验证了水平面海底和斜坡海底时，利用 RBD 方 参 考 文 献
法来估计信道 CIR 的有效性，并讨论了不同信噪比
[1] Dowling D R, Sabra K G. Acoustic remote sensing[J]. An-
和坡度下，RBD-CIR 与 CIR 理论值之间的平均互 nual Review of Fluid Mechanics, 2015, 47(1): 221–243.