Page 41 - 《应用声学》2020年第5期

第 39 卷 第 5 期 黎美琪等： 宽带多普勒测速技术中的发射信号 683

U ϕ (f) = V (f)C(f) 则s(t)的频谱S(f)为双边谱：
[ L−1 ] 1
∑ S(f) = (U ϕ (f − f 0 ) + U ϕ (f + f 0 )). (10)
= Tsinc(fT) e −jπfT c i e −j2πfiT . (5) 2
i=0 从式 (3)、式 (5) 可以看出，二相调制本质上相
˜
则 ˜s(t)的频谱S(f)为关于f = f 0 对称的正单边谱： 当于双极性码元幅度调制，U ϕ (f) 完全由码元幅度
˜
S(f) = U ϕ (f − f 0 ). (6) 调制函数 v(t) 及伪随机码序列 c i 决定，当单个码元
由Rectangle窗调制，V (f) = Tsinc (fT) e −jπfT ，对
实际上发射信号为实信号，伪随机二相编码信
˜
应的 S(f) 旁瓣高、衰减慢；c i 决定编码信号相关特
号的实数形式为 性，该特性已在大量文献中被讨论，不再细述。编码
信号时域波形可看作子矩形脉冲的叠加，频谱亦可
s(t) = cos(2πf 0 t + ϕ(t))
看作子脉冲频谱的叠加。从式 (10) 可以看出，实数
= cos(ω 0 t) cos(ϕ(t)) − sin(ω 0 t) sin(ϕ(t)), (7)
形式的伪随机二相编码信号，在频谱上表现为正负
由于sin(ϕ(t)) = 0， 单边谱的叠加，在以往学者的研究中往往忽略了负

1 ( j(ϕ(t)+ω 0 t) j(ϕ(t)−ω 0 t) 单边谱。
s(t) = e + e
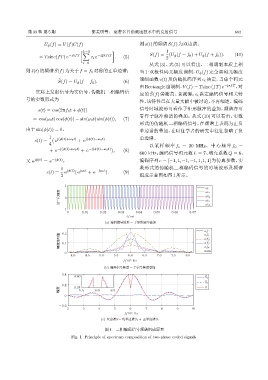
4 以采样频率 f s = 20 MHz、中心频率 f 0 =
+ e −j(ϕ(t)+ω 0 t) + e −j(ϕ(t)−ω 0 t) ) , (8)
600 kHz、编码信号码元数 L = 7、填充系数 Q = 6、
又 e jϕ(t) = e −jϕ(t) ， 编码序列 c = [−1, 1, −1, −1, 1, 1, 1] 为仿真参数，实
1 jϕ(t) jω 0 t −jω 0 t 数形式的伪随机二相编码信号的时域波形及频谱
s(t) = e ( e + e ). (9)
2 组成示意图如图1所示。

1
at
݂၂߄ږ؇ 0 at 
at 
at 
-1 at 
0 0.01 0.02 0.03 0.04 0.05 0.06 0.07
t/ms
(a) ᎄᆊηՂฉॎ=ߕᅾॎᑢфԯҫ

af
0.2
ࣨएፐࠫϙ 0.1 af 2
af 1
af 3
af 4
sum
0
4.0 4.5 5.0 5.5 6.0 6.5 7.0 7.5 8.0
f/10 Hz
5
(b) ᎄᆊηՂᮠ៨=ߕηՂᮠ៨ԯҫ
0.4
0.40 ~
S l
~
S r
ࣨए 0.2 0.35 5.5 6.0 6.5 S
0
-0.2
2 3 4 5 6 7 8 9 10
5
f/10 Hz
~ ~
(c) ԥ᣸៨S/᠇ӭ᣸៨S l ⇁ ൤ӭ᣸៨S r
图 1 二相编码信号频谱组成原理
Fig. 1 Principle of spectrum composition of two-phase coded signals