Page 44 - 《应用声学》2020年第5期

686 2020 年 9 月

1.0
X. ⊲ X. ⊲ X. ⊲ X.  Fc Rno
Y . ⊲
Y . 
Y . 
Y . 
0.8
ࣨएፐࠫϙ 0.6 Fc R
0.4
0.2
0
400 450 500 550 600 650 700 750 800
f/kHz
(a) Fc R
1.0
X: 585.8 S ~
݂၂߄ږ؇ፐࠫϙ 0.6 X: 521.5 X: 601.2 ~ S Rno
Y : 1
0.8
~ S Rno
~ S R
0.4
Y : 0.2547
0.2
Y : 0.07925
0 X: 507.4 Y : 0.3766
400 450 500 550 600 650 700 750 800
f/kHz
(b) ᧘ܭᎄᆊηՂᮠ៨
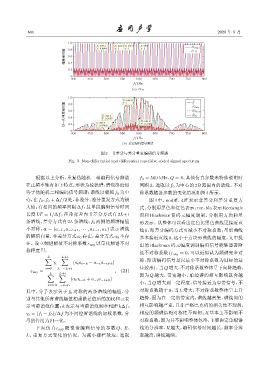
图 3 非差分与差分重复编码信号频谱
Fig. 3 Non-differential and differential repetitive coded signal spectrum

根据以上分析，重复伪随机二相编码信号频谱 f 0 = 500 kHz、Q = 4、其他仿真参数未特殊说明时
在正频率轴有如下特点：形状为梳状谱，谱包络近似 同图3。选取以f 0 为中心的2B 范围内的谱线。不对
等于伪随机二相编码信号频谱；谱线以载频f 0 为中 称系数随各参数的变化情况如图4所示。

心，在f 0 、f 0 + ∆f/2处，非差分、差分重复方式为极 图 4 中，nodiff、diff 表示非差分和差分重复方
大值；有相同的频率间隔 ∆f，且单段编码信号时间 式，分别用黑色和红色表示；rec、bla 表示 Rectangle
长度 LT = 1/∆f；在带宽 B 内非差分方式有 2L+1 窗和 Blackman 窗码元幅度调制，分别用方块和星
条谱线、差分方式有 2L 条谱线；f 0 两侧的频谱幅值 形表示。从整体可以看出红色比黑色曲线更接近直
不对称，a = (a −L , a −L+1 , · · · , a L−1 , a L ) 表示谱线 线0，即差分编码方式可减小不对称系数；星形曲线
的幅值向量，非差分方式 a 0 存在，差分方式 a 0 不存 基本接近直线 0，远小于方块形曲线的幅度，文中提
在。设立频谱幅值不对称系数 ε asy 以量化频谱不对 出的 Blackman 码元幅度调制编码信号能够显著降
称程度 [1] ： 低不对称系数 (ε asy ≈ 0，可以近似认为频谱完全对
L L+i
∑ ∑ 称，即该编码信号是以最小不对称系数为目标的最
(a i a i−k − a −i a −i+k )
γ i
i=0 k=−L+i 佳波形)。当Q增大，不对称系数整体呈下向降趋势，
ε asy = , (21)
L L+i
∑ ∑ 因为 Q 越大，带宽越小，单边谱的相互影响就会越
(a i a i−k + a −i a −i+k )
小，当Q 增大到一定程度，信号接近为窄带信号，不
i=0 k=−L+i
其中，分子表示关于 f 0 对称的两条谱线的幅值，分 对称系数趋于 0；当L 增大，不对称系数整体呈上升
别与其他所有谱线幅值相乘做差值后的加权和；i表 趋势，因为在一定的带宽内，谱线越密集，谱线间的
示当前谱线位置；k 表示与当前谱线频率相距 k∆f； 相互影响越严重，且非严格巴克码的相关性不理想，
γ i = (f i − f 0 )/∆f 为不同位置谱线的加权系数，分 相应的频谱结构对称性不理想；R 基本上不影响不
母的作用为归一化。 对称系数，因为其不影响整体包络，主要决定单根谱
下面仿真 ε asy 随宽带编码信号的参数 Q、R、 线的分辨率，R 越大，编码信号时间越长，频率分辨
L、重复方式变化的情况。为减小栅栏效应，选取 率越高，谱线越细。