Page 46 - 《应用声学》2020年第5期

688 2020 年 9 月

表 1 4 种编码信号的不对称系数 系数相似的规律。图6(a) 表明：Blackman窗码元调
Table 1 Asymmetry coefficients of four 制信号对应的测频偏差小于 Rectangle 窗码元调制
coded signals 信号；差分重复方式信号对应的测频偏差小于非
编码信号 nodiff+rec diff+rec nodiff+bla diff+bla 差分重复方式，高信噪比时，diff+rec 较 nodiff+rec
ε asy 0.56 −0.16 −0.0007 −0.0004 的相对测频偏差降低了约 2‰, diff+bla 相比 nod-
由表 1 知，Blackman码元幅度调制宽带编码信 iff+bla 在偏差上的优势不明显。图 6(b) 表明：低
号的不对称系数较 Rectangle 码元幅度调制低 3 个 信噪比时，Blackman 窗码元调制信号对应的测频
数量级，差分重复方式较非差分方式具有更小的不 标准差明显小于 Rectangle 窗码元调制信号。总的
对称系数。Blackman 窗码元调制信号的不对称性 来看，diff+bla 具有最好的测频性能，其与传统的
系数已经很小，故差分重复方式对不对称系数的影 nodiff+rec相比：信噪比在 0 ∼ −10 dB 范围内测频
响不大，差分重复方式在 Rectangle 窗码元调制信 标准差约下降 2% ∼ 20%；信噪比高于 10 dB 时相
号中表现出较明显的优势。差分重复 Blackman 码 对测频偏差约小5‰ ∼ 6‰。
元幅度调制宽带编码信号具有最小的不对称系数。 综合表 1 的不对称系数值及图 6 的测频误差分
由图 6 可以看出，不考虑波束开角的点回波模 析可知：不对称系数越小，测频偏差、标准差均越小，
型下，基于复协方差法的测频性能具有与不对称 即测频性能更佳。

2.0
nodiff+rec
฾ᮠϠࣀፐࠫϙ/Hz 1.0 X: 20 diff+bla
diff+rec
1.5
nodiff+bla
Y : 0.7066
0.5
X: 20
Y : 0.09535
0
-10 -5 0 5 10 15 20 25 30
η٪උ/dB
(a) ϠࣀˁᎄᆊηՂТጇ
60
nodiff+rec
diff+rec
nodiff+bla
ಖюࣀ/Hz 20
40
diff+bla

0
-10 -5 0 5 10 15 20 25 30
η٪උ/dB
(b) ಖюࣀˁᎄᆊηՂТጇ
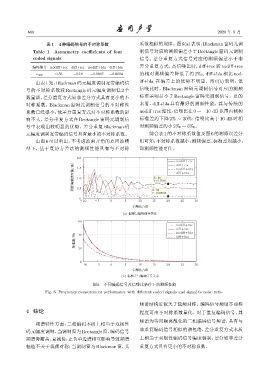
图 6 不同编码信号及信噪比条件下的测频性能
Fig. 6 Frequency measurement performance with different coded signals and signal to noise ratio

频谱结构近似关于载频对称。编码信号频谱不对称
4 结论 程度可由不对称系数量化。对于重复编码信号，其

频谱为等间隔离散化的二相编码信号频谱，具有与
频谱特性方面：二相编码本质上相当于双极性
非重复编码信号相似的谱包络，差分重复方式本质
码元幅度调制，当调制窗为 Rectangle 窗，编码信号
频谱旁瓣高、衰减慢，正负单边谱相互影响导致频谱 上相当于双极性编码信号幅度调制，差分较非差分
幅值不关于载频对称；当调制窗为 Blackman窗，其 重复方式具有更小的不对称系数。