Page 51 - 《应用声学》2020年第5期

第 39 卷 第 5 期 谭靖骞等： 北极海域海洋环境噪声建模与特性分析 693

1.1 2.1 非高斯性判定
1.0 统计理论中的偏度、峰度以及方差是描述噪声
લՌएࠫඋ,
0.9 SNR=5 dB 分布的统计量，可用于初步判定噪声数据的非高斯
R_square 0.8 性。峰度大于3，说明噪声的分布与高斯噪声相比具
有更尖的峰顶，反之则具有平峰值；偏度是统计数据
0.7
分布非对称程度的数字特征，与 α 稳定分布中参数
0.6
ᰴளѬ࣋લՌ β 存在一定对应关系，其值为 0 时表征分布具有对
0.5 αሷࠀѬ࣋લՌ
称性；方差是衡量数据离散程度的重要参数，可以根
0.4 据实测数据中样本方差的收敛性来判定该数据样
0 0.2 0.4 0.6 0.8 1.0
фѤηՂӴඋ 本是否具有高斯性。在α 稳定分布中，当α = 2时分
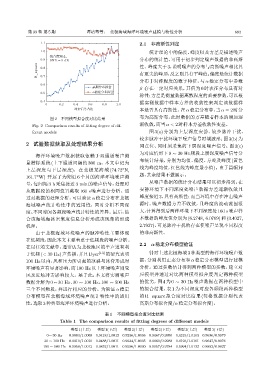
图 2 不同模型拟合度对比结果 布为高斯分布，此时数据的方差随着样本的增加逐
Fig. 2 Comparison results of fitting degree of dif- 渐收敛，而当α < 2时样本方差收敛性变差。
ferent models 图 3(a) 分别为上层深度安静、较少脉冲干扰、
较多脉冲干扰环境下噪声信号时域波形；图3(b) 为
2 试验数据获取及处理结果分析 同点位、同时刻采集的下层深度噪声信号；图 3(c)

为对应情形下 0 ∼ 30 Hz 频段上层深度噪声信号分
海洋环境噪声数据获取依赖于双通道噪声测
布统计结果，分别为均值、偏度、方差及峰度 (黄色
量潜标系统 (上下通道间隔约 300 m，本文中记为
线为峰度均值，红色线为峰度最小值)。由于篇幅问
上层深度与下层深度)，在北极某海域 (74.72 N,
◦
161.7 W) 开展了为期近 6 个月的海洋环境噪声测 题，其余结果不做展示。
◦
量，每间隔 3 h 采集接近 3 min 的噪声信号，处理时 从噪声数据的统计分布结果可以初步得到，在
从数据段的相同位置截取 160 s 噪声进行分析。通 安静环境下不同深度处噪声数据方差逐渐收敛且
过对数据的处理分析，可以验证 α 稳定分布在北极 峰度接近 3，具有高斯性；而当环境中存在冲击噪声
海域噪声统计特性中的适用性，同时分析不同深 源时，噪声数据方差不收敛，且峰度的波动范围很
度、不同时间各频段噪声统计特性的差异。最后，结 大，计算得到后两种环境下不同深度处160 s噪声样
合该海域海冰密集度信息分析形成该现象的形成 本数据的峰度值分别为(6.2748, 6.0769) 和(3.4027,
机理。 2.7937)，可见脉冲干扰的存在使噪声呈现不同程度
由于北极海域环境噪声的脉冲特性主要体现 的非高斯性。
在低频段，因此本文主要着重于低频段的噪声分析。
2.2 α稳定分布模型验证
在以往的文献中，通常认为北极地区的半声道有利
于低频(< 30 Hz)声传播，并且 Dyer [13] 的研究表明 针对上述北极海域3 种类型的海洋环境噪声数
100 Hz 以内，风和压力所引起的冰裂与冰脊形成对 据，分别利用正态分布和 α 稳定分布模型进行建模
环境噪声有显著影响，而100 Hz 以上环境噪声则受 分析。通过参数估计得到两种模型的参数，建立对
风及近场冲击影响较大。基于此，本文将实测噪声 应模型并通过对比两种模型拟合度判定两种模型
数据分解为 0 ∼ 30 Hz、30 ∼ 100 Hz、100 ∼ 500 Hz 的优劣，图 4 为 0 ∼ 30 Hz 噪声数据在两种模型中
三个不同频段，并进行相应的分析。为验证 α 稳定 的拟合结果，表 1 为不同深度对应各频段两种模型
分布模型在北极海域环境噪声统计特性中的适用 的 R_square 拟合度对比结果 (每格数据分别代表
性，选取3种典型海洋环境噪声进行分析。 高斯分布拟合度/α 稳定分布拟合度)。

表 1 不同模型拟合度对比结果
Table 1 The comparison results of fitting degrees of different models

类型 1(上层) 类型 1(下层) 类型 2(上层) 类型 2(下层) 类型 3(上层) 类型 3(下层)
0∼ 30 Hz 0.9884/1.0009 0.9418/1.0012 0.9236/1.0006 0.9667/0.9990 0.6215/1.0163 0.9696/0.9979
30 ∼ 100 Hz 0.9910/1.0010 0.9488/1.0011 0.9234/1.0005 0.9660/0.9988 0.6193/1.0161 0.9647/0.9976
100 ∼ 500 Hz 0.9958/1.0012 0.9852/1.0011 0.9296/1.0000 0.9057/0.9784 0.5994/1.0132 0.8852/0.9827