Page 50 - 《应用声学》2020年第5期

692 2020 年 9 月

2
α
的一致估计器如下： 其中，y k = lg(− lg | ˆφ(t)| )，m = lg(2γ )，w k =
n
1 ∑ lg |t k |，ε k 是均值为零的独立同分布误差项，实数集
ˆ φ(t) = exp(jtx k ). (3)
n t k = πk/25, k = 1, 2, · · · , K。根据α 和样本容量不
k=1
因此，根据式(2)、式(3)，令y = lg(− lg |φ(t)| )， 同K ∈ [9, 134]，由式(4)则可以估计出 ˆα 和 ˆγ。
2
则参数α 和γ 可通过如下线性回归估计得到： 当 α ̸= 1 时， 特征函数 φ(t) 的实部和虚部
y k = m + αw k + ε k , (4) 分别为

 [ ( πα )]
α
α
Re {φ (t)} = exp (− |γt| ) cos δt − |γt| βsign (t) tan ,


 2
α ̸= 1. (5)
[ ( )]
 πα
 α α
Im {φ (t)} = exp (− |γt| ) sin δt − |γt| βsign (t) tan ,

2
因此，可以得到 1.2 数值仿真分析
( )
Im{φ(t)} α πα
arctan =δt−|γt| βsign(t) tan . 根据北极海域环境噪声的非高斯性，为验证 α
Re{φ(t)} 2
稳定分布模型的建模效果，进行理论仿真分析。仿
(6)
真中向高斯白噪声中加入信噪比为 5 dB、冲击信
则进一步，结合式 (4)估计的 α 与γ，参数 β 和δ 号占比不同的脉冲干扰，并以核密度估计 (Kernel
可通过如下线性回归估计得到： density estimation, KDE)为参照，利用检验预测模
( πα )
α
α
z l =δu l − βγ tan · sign (u l ) |u l | +η l , (7) 型时常用的 R_square 指标分析高斯分布与 α 稳定
2
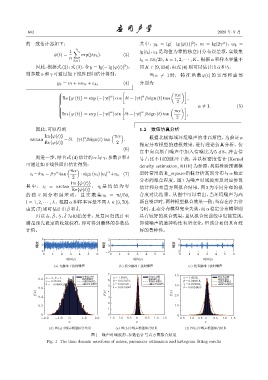
分布的拟合程度。图 1 为噪声时域波形及对应参数
Im { ˆφ (t)}
其 中， z l = arctan ， η l 是 均 值 为 零 估计和分布直方图拟合结果，图 2 为不同分布的拟
Re{ ˆφ(t)}
的 独 立 同 分 布 误 差 项， 且 实 数 集 u l = πl/50, 合度对比结果。从图中可以看出，当环境噪声为高
l = 1, 2, · · · , L。根据 α 和样本容量不同 L ∈ [9, 70]， 斯白噪声时，两种模型拟合效果一致；当存在冲击信
ˆ
ˆ
由式(7)则可估计出β 和δ。 号时，正态分布模型完全失效，而α 稳定分布模型则
ˆ
ˆ
再以 ˆα、β、ˆγ、δ 为初始条件，反复回归统计至 具有较好的拟合效果，且从拟合度曲线中也能发现，
满足预先设定的收敛标准，即可得到最终的参数估 即使噪声的脉冲特性有所变化，但该分布仍具有较
计值。 好的鲁棒性。
2 2 2
ࣨए 0 ࣨए 0 ࣨए 0
-2 -2 -2
0 1 2 3 4 5 6 0 1 2 3 4 5 6 0 1 2 3 4 5 6
௑ᫎ/s ௑ᫎ/s ௑ᫎ/s
(a) ௄ᑢфࣰ੸௑٪ܦ (b) ᣗ࠶ᑢфࣰ੸௑٪ܦ (c) ᣗܳᑢфࣰ੸௑٪ܦ
7 4.0
Ѭ࣋ᄰவڏ α=1.6082, Ѭ࣋ᄰவڏ α=1.4326, Ѭ࣋ᄰவڏ
0.8 α=2, β=1, ಩ࠛएͥᝠ ಩ࠛएͥᝠ ಩ࠛएͥᝠ
γ=0.35384, ൤গѬ࣋લՌ 6 β=0.037472, ൤গѬ࣋લՌ β=0.048918, ൤গѬ࣋લՌ
δ=-0.0066423 αሷࠀѬ࣋લՌ 5 γ=0.041331, αሷࠀѬ࣋લՌ 3.0 γ=0.079652, αሷࠀѬ࣋લՌ
0.6 δ=0.0013049 δ=0.0024455
f↼x↽ f↼x↽ 4 f↼x↽
0.4 3 2.0
2
0.2 1.0
1
0 0 0
-2.0 -1.0 0 1.0 2.0 -1.5 -1.0 -0.5 0 0.5 1.0 1.5 -1.5 -1.0-0.5 0 0.5 1.0 1.5
x x x
(d) ڏ(a)˗٪ܦവیલՌፇ౧ (e) ڏ(b)˗٪ܦവیલՌፇ౧ (f) ڏ(c)˗٪ܦവیલՌፇ౧
图 1 噪声时域波形、参数估计与直方图拟合结果
Fig. 1 The time domain waveform of noises, parameter estimation and histogram fitting results