Page 45 - 《应用声学》2020年第5期

第 39 卷 第 5 期 黎美琪等： 宽带多普勒测速技术中的发射信号 687

2
ˀࠫሦጇ஝ 0 nodiff+rec

diff+rec
-2
nodiff+bla
diff+bla
-4
2 4 6 8 10 12 14 16
Q
(a) ˀࠫሦጇ஝ˁQТጇ
10
ˀࠫሦጇ஝ 0

-10
0 10 20 30 40 50 60 70
L
(b) ˀࠫሦጇ஝ˁLТጇ

2
ˀࠫሦጇ஝ 1 0

-1
2 3 4 5 6 7 8 9 10
R
(c) ˀࠫሦጇ஝ˁRТጇ
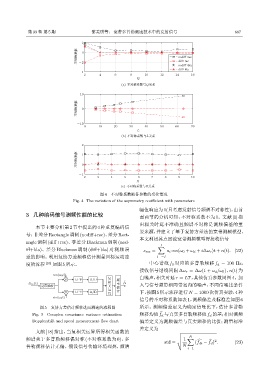
图 4 不对称系数随各参数的变化情况
Fig. 4 The variation of the asymmetry coefficient with parameters
幅值响应为1(只考虑发射信号频谱不对称性)，由前
3 几种编码信号测频性能的比较 面两节的分析可知，不对称系数不为 0。文献 [1] 指
出相关时延不准确且频谱不对称是测频偏差的重
本节主要分析第 2 节中提出的 4 种重复编码信
要来源，并建立了基于复协方差法的宽带测频模型，
号：非差分 Rectangle 调制 (nodiff+rec)、差分 Rect-
本文利用其点回波宽带测频模型得接收信号
angle 调制 (diff+rec)、非差分 Blackman 调制 (nod-
I
iff+bla)、差分 Blackman 调制 (diff+bla) 对测频误 s rec = ∑ a i cos(ω 0 + ω d + i∆ω r )t + n(t). (22)
差的影响。利用复协方差频移估计测量目标运动速 i=−I
度的流程 [10] 如图5所示。 中心谱线 f 0 对应的多普勒频移 f d = 100 Hz，
接收信号谱线间隔 ∆ω r = ∆ω(1 + ω d /ω 0 )，n(t) 为
cos(ω 0t)
LPF A/D ܭ ᮠ 白噪声，相关时延 τ = LT，其他仿真参数同图 4。加

⌣
S rec (t) ᄱ ဋ f d
ࠕࣜ໚ฉ Т ͥ 入与信号频带相同带宽内的噪声，不同信噪比条件
ᤂ
LPF A/D ካ ᝠ 下，按图5所示流程进行N = 1000次仿真实验，4种
sin(ω 0t)
信号的不对称系数如表 1，测频偏差及标准差如图 6
图 5 复协方差估计频移进而测速的流程图 所示。测频偏差定义为确定信噪比下，估计多普勒
Fig. 5 Complex covariance variance estimation 频移均值f d 与真实多普勒频移值f d 的差；相对测频
b
Dopplershift and speed measurement flow chart 偏差定义为测频偏差与真实频移的比值；测量标准
差定义为
文献 [18] 指出，当复相关运算所得相关函数的 v
u N
频谱关于多普勒频移偶对称 (不对称系数为 0)，多 u 1 ∑
b 2
std = t (f di − f d ) . (23)
c
普勒频移估计无偏。假设信号传输环境理想，频谱 N i=1