Page 35 - 《应用声学》2020年第5期

第 39 卷 第 5 期 张雪冬等： 斜坡海底波导中随机声源的信道盲解卷积 677

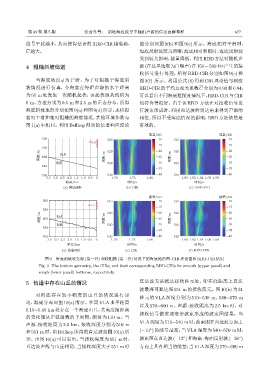
信号干扰越小，从而使得估计的 RBD-CIR 越准确， 值分别如图 9(b) 和图 9(e) 所示。海底相对平滑时，
C 越大。 海底反射波较为清晰；海底相对粗糙时，海底反射波
受到较大影响，能量降低。利用RBD 方法对随机声
4 粗糙斜坡信道 源(在这里选取为白噪声)在150 ∼ 500 Hz产生的接
收信号进行处理，所得 RBD-CIR 分别如图 9(c) 和
当海底坡度 ϕ 为 1 时，为了对粗糙平海底斜 图 9(f) 所示。利用公式 (8) 得到 CIR 理论值与相应
◦
坡情况进行仿真，令海底在每距声源的水平距离 RBD-CIR 的平均互相关系数 C 分别为 0.93 和0.94，
为 50 m 处发生一次随机起伏，该起伏服从均值为 可以看出不同海底粗糙度情况下，RBD-CIR与CIR
0 m、方差分别为 0.5 m 和 2.5 m 的正态分布，所得 均符合得很好。由于该 RBD 方法在对接收信号进
海底斜坡地形分别如图 9(a) 和图 9(d)所示，来模拟 行波束形成时，利用直达波的到达角来得到声源的
相对平滑和相对粗糙的海底情况，其他环境参数与 相位，所以不受海底情况的影响，RBD 方法依然是
图 1(a) 中相同。利用 Bellhop 得到的信道响应理论 有效的。

ᑟ᧚/dB ᑟ᧚/dB
500 510 -10 510 -10
VLA
-15 -15
550 -20 -20
ງए/m 600 ๒ඵ ງए/m 520 -25 ງए/m 520 -25

๒अ 530 -30 530 -30
650
-35 -35
700 540 -40 540 -40
3.5 3.0 2.5 2.0 1.5 1.0 0.5 0 1.70 1.75 1.80 1.00 1.02 1.04 1.06 1.08
ᡰሏ/km ௑ᫎ/s ௑ᫎ/s
(a) ๒अڡॎ (b) CIR (c) RBD-CIR
ᑟ᧚/dB ᑟ᧚/dB
500 510 -10 510 -10
VLA
-15 -15
550 520 -20 520 -20
ງए/m 600 ๒ඵ ງए/m -25 ງए/m -25

๒अ 530 -30 530 -30
650
-35 -35
700 540 -40 540 -40
3.5 3.0 2.5 2.0 1.5 1.0 0.5 0 1.70 1.75 1.80 1.00 1.02 1.04 1.06 1.08
ᡰሏ/km ௑ᫎ/s ௑ᫎ/s
(d) ๒अڡॎ (e) CIR (f) RBD-CIR
图 9 海底斜坡较光滑 (第一行) 和较粗糙 (第二行) 情况下的海底地形图、CIR 理论值和 RBD-CIR 结果
Fig. 9 The bottom geometry, the CIRs, and their corresponding RBD-CIRs for smooth (upper panel) and
rough (lower panel) bottoms, respectively

5 信道中存在山丘的情况 直达波无法抵达接收阵元处，即在此距离上直达
波最深可抵达深 551 m 的接收阵元。图 10(b) 为 31
对海底存在较小幅度的山丘的情况进行讨
阵元的 VLA 深度分别为 510∼540 m、540∼570 m
论，海底分布如图 10(a) 所示。在离 VLA 水平距离
以及 570∼600 m，声源 -接收距离为 2.5 km 时，对
0.15∼0.40 km 处存在一个海底山丘，其高度随距离
接收信号做常规宽带波束形成的波束图结果。当
的变化服从正弦函数的半周期，幅值为 110 m。当
VLA深度为510∼540 m时，波束图在直达波方向上
声源 -接收距离为 2.5 km、接收深度分别为 510 m
◦
和 551 m 时，由Bellhop 所得的直达波如图 10(a) 所 (−13 ) 的能量最高；当 VLA 深度为 540∼570 m 时，
◦
◦
示。由图 10(a) 可以看出，当接收深度为 551 m 时， 波束图在直达波(−13 )和海底-海面反射波(−36 )
直达波声线与山丘相切，当接收深度大于 551 m 时 方向上具有相当的能量；当VLA深度为570∼600 m