Page 30 - 《应用声学》2020年第5期

672 2020 年 9 月

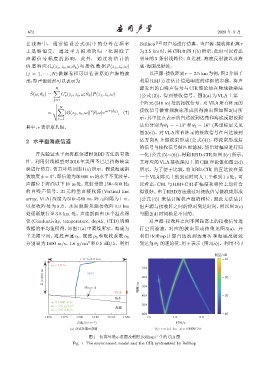
在浅海 中， 通常假 设公 式 (6) 中的分母 在频率 Bellhop [12] 对声场进行仿真。当声源 -接收阵距离 r
上 足 够 恒 定， 通 过 平 方 根 项 的 归 一 化 消 除 了 为 2.5 km 时，其 CIR 如图 1(b) 所示，此时可以看出
声 源 信 号 幅 度 的 影 响。 此 外， 通 过 将 估 计 的 明显的 3 条射线路径：直达波、海底反射波以及海
信道响应 G e (z j , z s , ω; θ k ) 与接收数据 P(z j , z s , ω) 底-海面反射波。
(j = 1, · · · , N) 做解卷积可以估计原始声源的波 以声源-接收距离r = 2.5 km为例，图2介绍了
形，即声源波形可以表示为 利用 RBD 方法估计信道响应的详细的步骤。将声
N 源发出的白噪声信号与 CIR 理论值在频域做乘法
∑
ˆ
∗
S(ω; θ k ) = G (z j , z s , ω; θ k )P(z j , z s , ω) (公式 (2))，得到接收信号。图 2(a) 为 VLA 上第一
e
j=1
个阵元(510 m)处的接收信号。对VLA所有阵元的
v
N
u
u∑ 2 iωT (θ k ) 接收信号做常规波束形成所得波束图如图 2(b) 所
= t |G(z j , z s , ω)| S(ω)e , (7)
示，其中红点表示的直达波到达角和海底反射波到
j=1
◦
◦
其中，∗表示取共轭。 达角分别为 θ 1 = −13 和 θ 2 = 16 (其坐标定义见
图 2(e))。对 VLA 所有阵元的接收信号在直达波到
2 水平面海底信道 达方向 θ 1 上做波束形成 (公式 (4))，将波束形成后
的信号与接收信号做匹配滤波，然后对幅度进行归
首先验证水平面海底信道时 RBD 方法的有效 一化(公式(5)∼(6))，得到RBD-CIR如图2(c)所示。
性。利用射线模型对 2016 年美国圣巴巴拉海峡实 其对应的 VLA 接收深度上的 CIR 理论值如图 2(d)
验进行仿真，仿真环境如图 1(a) 所示。假设海底斜 所示。为了便于比较，将 RBD-CIR 的直达波在第
坡坡度ϕ = 0 ，即信道为深600 m的水平不变波导。 一个 VLA 阵元上的到达时间人工平移到 1 s 处。可
◦
声源位于海面以下 10 m 处，发射带宽 150∼500 Hz 以看出，CIR 与 RBD-CIR 在幅度和相位上均符合
的白噪声信号。31 元的垂直接收阵 (Vertical line 得很好。由于RBD方法通过对接收信号做波束形成
array, VLA) 深度为 510∼540 m，阵元间隔为 1 m。 (公式 (4)) 来估计随机声源的相位，因此无法估计
以接收阵处为 0 点，水面舰船从距接收阵 1.0 km 出声源与接收阵之间的绝对到达时间，所以图 2(c)
处逐渐航行至 3.5 km 处。声速剖面由 16 个温盐深 与图2(d)时间轴是不同的。
仪 (Conductivity, temperature, depth, CTD) 所测 对声源 -接收阵之间不同距离上的接收信号进

数据的平均值所得，如图 1(a) 中蓝线所示。海底为 行空间滤波，对应的波束形成结果见图 3(a)，并
利用 Bellhop 计算直达波到达角 θ 1 和海底反射波
半无限空间，海底声速 c b 、密度 ρ b 和吸收系数 α b
3
分别设为 1600 m/s、1.6 g/cm 和 0.5 dB/λ。利用 到达角θ 2 的理论值，用+表示 (图3(a))。利用不同
ᑟ᧚/dB
r=1~3.5 km -10
z s=10 m
100
D=600 m SSP 200 -20

Slope φ ງए/m 300
VLA
400 -30
๒ඵ
c b=1600 m/s
ρ b =1.6 g/cm 3 ๒अ 500
α b =0.5 dB/λ
600 -40
1450 1470 1490 1510 1530 1550 1.6 1.8 2.0
ܦᤴ/(mSs -1 ) ௑ᫎ/s
(a) ͌ᄾဗܒᇨਓڏ (b) r=2.5 km, φ=0O௑ᄊCIR

图 1 仿真环境示意图及利用 Bellhop 产生的 CIR 图
Fig. 1 The environment model and the CIR synthesized by Bellhop