Page 8 - 《应用声学》2020年第5期

650 2020 年 9 月

径的预选择算法的时间复杂度为 O (MN)，和整个 其中，σ 2 和 σ 2 为测量误差在深度和距离方向的
a D a R
空间中点的个数呈线性关系，而当每次迭代更新路 标准差，B 的值为
径时，需要的计算时间复杂度仅为 O (N)。这种只  ∆t 2 
0
与前一轮计算的结果相关的无后效性有利于减少  2 2 


 ∆t 
大数据集和在线运算情况下的计算复杂度。  0  (13)
B =  2  .
 
 ∆t 0 
 
134
ϋᤥ᡹य़ 0 ∆t
௑णጳ
167 以每一个预选择路径上的点 a k 作为目标状态的观
测，设测量误差为u k ，则a k 可以表示为
ງए/m 200 a k = Hx k + u k . (14)
233
由于是在笛卡尔坐标系下进行测量，观测矩阵 H
266 是一个单位阵。u k 的协方差矩阵中值的大小和选

择路径的深度分辨率有关：深度分辨率越高，值应
3 4 5 6
ᡰሏ/km 被设置的越小；深度分辨率越低，值应被设置的越
大。使用卡尔曼滤波算法后的效果如图4所示。图4
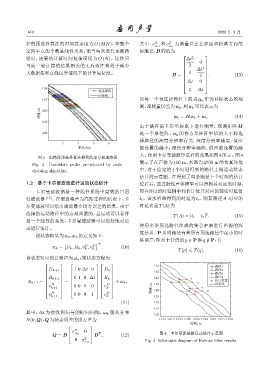
图 3 由路径预选择算法得到的部分候选路径
展示了在声源为 150 m、水深为4700 m 的仿真环境
Fig. 3 Candidate paths pre-selected by path
choosing algorithm 中，对于给定的 4 个时延得到的路径上做运动状态
估计的示意图。在得到了每条路径下个时刻的估计
1.2 基于卡尔曼滤波进行运动状态估计 位置后，通过射线声学模型可以得到其对应的时延，
卡尔曼滤波器是一种线性系统中高效的自回 即在图 2的时延图中和估计位置对应的理论时延值
归滤波器 [15] 。在假设噪声为高斯过程的情况下，卡 t t 。设水听器得到的时延为 t r ，则某路径 A 对应的
尔曼滤波可以给出满足最小均方误差的结果。由于 时延误差T(A)为
选择的运动路径中的点是离散的，且运动可以看作 2
T(A) = |t t − t r | . (15)
是一个线性的系统，卡尔曼滤波器可以很好地对运
使用多条预选路径组成的集合 P 来进行声源的深
动进行估计。
度估计。P 里的路径有着所有预选路径中最小的时
设状态向量为x k ，x k 的定义如下：
延误差，即对于任意的p ∈ P和q ̸∈ P，有
[ R D ] T
x k = D k , R k , v , v . (10)
k k
T(p) 6 T(q). (16)
设状态对应的白噪声为ω k ，则状态方程为

     
133 ᡹य़1
1 0 ∆t 0
D k+1 D k ᡹य़2
      137
᡹य़3
      ᡹य़4
 R k+1   0 1 0 ∆t   R k  141
x k+1 =   =     + ω k , ͥᝠͯᎶ
 D     D  145 ௑णጳ
 v  0 0 1 0   v
k+1  k  ງए/m
      149
v R 0 0 0 1 v R
k+1 k 153
(11) 157
161
其中，∆t 为接收到信号的时间间隔，ω k 服从分布
165

N(0, Q)，Q为状态误差的协方差为 1191 1217 1243 1270 1296 1322 1348 1374 1400
ᡰሏ/m
 
σ 2 0 卡尔曼滤波做运动估计示意图
T
Q = B  a D  B , (12) 图 4
0 σ 2 Fig. 4 Schematic diagram of Kalman filter results
a R