Page 124 - 《应用声学》2021年第2期

292 2021 年 3 月

的增大，系统性能会有所下降，这主要是因为导频间 由于单一的基于 CS 的限幅失真补偿算法受信
隔对信道估计LS算法有较大影响，从而会影响误差 道估计的影响较大，本文采用的 CS 与 LS 信道估计
阈值ε的判断。 相结合的优化算法，可以在减小限幅失真的同时提
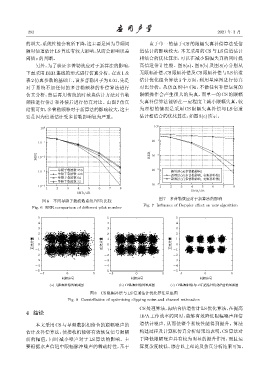
另外，为了验证多普勒效应对于新算法的影响， 高信道估计性能。图 8(a)、图 8(b) 及图 8(c) 分别从
下面采用BER曲线的形式进行仿真分析。在表1及 无限幅补偿、CS限幅补偿及CS限幅补偿与LS信道
表2 仿真参数的基础上，设多普勒因子为0.01，先是 估计优化组合算法 3 个方面，利用星座图进行仿真
对于系统不加任何的多普勒频移的补偿算法进行 对比分析。从仿真图中可知，不做任何补偿运算的
仿真分析，然后再用传统的时域块估计方法对普勒 限幅操作会产生很大的失真，而单一的 CS 的限幅
频移进行估计和补偿后进行仿真对比。由图 7 仿真 失真补偿算法能够在一定程度上减小限幅失真，较
结果可知，多普勒频移对于新算法的影响较大，这主 为理想的情况是采用 CS 限幅失真补偿与 LS 信道
要是因为信道估计受多普勒影响较为严重。 估计相结合的优化算法，如图8(c)所示。

10 0 10 0

10 -1
10 -1
BER 10 -2 BER 10 -2

10 -3 ࠮ᮠߕᣒฉ஝ 256 10 -3 ழካข(௄ܳ௿ҿॖ־)
࠮ᮠߕᣒฉ஝ 128 ழካข(దܳ௿ҿॖ־, దᮠረᛪϪ)
࠮ᮠߕᣒฉ஝ 64 ழካข(దܳ௿ҿॖ־, ௄ᮠረᛪϪ)
࠮ᮠߕᣒฉ஝ 32
10 -4
10 -4 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8
SNR/dB
SNR/dB
图 7 多普勒效应对于新算法的影响
图 6 不同导频子载波数系统 BER 比较
Fig. 7 Influence of Doppler effect on new algorithm
Fig. 6 BER comparison of different pilot number
5 5 5
4 4 4
3 3 3
2 2 2
൤̔Ѭ᧚ 1 0 ൤̔Ѭ᧚ 1 0 ൤̔Ѭ᧚ 1 0

-1
-2 -1 -1
-2
-2
-3 -3 -3
-4 -4 -4
-5 -5 -5
-5 0 5 -5 0 5 -5 0 5
ՏᄱѬ᧚ ՏᄱѬ᧚ ՏᄱѬ᧚
(a) ௄ᬍࣨᛪϪᄊ௡ऐڏ (b) CSᬍࣨᛪϪᄊ௡ऐڏ (c) CSᬍࣨᛪϪˁLSη᥋ͥᝠ͖ӑፇՌᄊ௡ऐڏ

图 8 CS 限幅补偿与 LS 信道估计优化算法星座图
Fig. 8 Constellation of optimizing clipping noise and channel estimation

CS处理算法，再结合信道估计LS优化算法，在提高
4 结论
HPA工作效率的同时，能够有效降低限幅噪声和信
本文采用 CS 与导频数据相给合的限幅噪声的 道估计噪声，从而使整个系统性能得到提升。算法
估计及补偿算法，使接收机能够有效恢复信号限幅 构建过程及计算机仿真分析结果均表明，CS算法对
前的幅值，同时减小噪声对于 LS 算法的影响。主 于降低限幅噪声具有较为明显的提升作用，而且运
要根据水声信道中限幅脉冲噪声的稀疏特性，基于 算复杂度较低。综合以上理论及仿真分析结果可知，