Page 65 - 《应用声学》2021年第2期

第 40 卷 第 2 期 田野等： 数控裁剪机切割刀壳体振动噪声预测分析 233

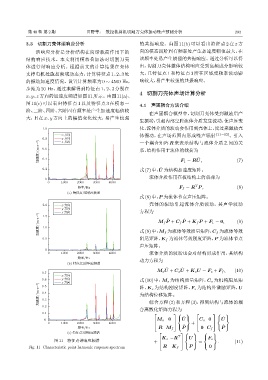
3.3 切割刀壳体谐响应分析 的共振响应。由图 11(b) 可以看出特征点 2 在 x 方
谐响应分析是分析结构在简谐载荷作用下的 向的模态四阶固有频率处产生加速度幅值最大，在
结构响应技术。本文利用模态叠加法对切割刀壳 该频率处易产生较强的共振响应。通过分析可以得
体进行谐响应分析。根据前文的计算结果在壳体 出，切割刀壳体整体结构响应受到高频成分影响较
支撑电机处施加频域动态力，计算特征点 1、2、3 处 大，且特征点 1 和特征点 3 所在区域受频率波动影
的振动加速度情况。设置计算频率为 0 ∼ 4500 Hz， 响较大，易产生较强的共振响应。
步距为 20 Hz，通过求解得到特征点 1、2、3 分别在
4 切割刀壳体声场计算分析
x、y、z 方向的加速度频谱如图 11所示。由图 11(a)、
图 11(c) 可以看出特征点 1 以及特征点 3 在模态一 4.1 声固耦合方法介绍
阶、二阶、四阶、六阶固有频率处产生加速度幅值较
在声固耦合模型中，切割刀壳体受到激励后产
大，且在 x、y 方向上的幅值变化较大，易产生较强
生振动，引起内部空腔流体介质发生波动，使声压变
1.0 化，流体介质的波动会作用到壳体上，反过来激励壳
x வՔ 体振动，在声场范围内形成噪声辐射 [11−12] 。引入
0.8 y வՔ 一个耦合矩阵 R 来表示结构与流体介质之间的关
ҫᤴए/(mSs -2 ) 0.6 系，结构作用于流体的载荷为 ¨ (7)
z வՔ

0.4
F 1 = RU,
¨
0.2 式(7)中，U 为结构加速度矩阵。
流体介质作用在板结构上的载荷为
0
0 1000 2000 3000 4000
T
ᮠဋ/Hz F f = R P , (8)
(a) ྲढ़ག1ៈ־ऄᮠ៨
式(8)中，P 为流体节点声压矩阵。
2.0 x வՔ 壳体的振动引起流体介质波动，其声学波动
y வՔ
z வՔ 方程为
ҫᤴए/(mSs -2 ) 1.0 式(9) 中：M f 为流体等效质量矩阵，C f 为流体等效
1.5
˙
¨
(9)
M f P + C f P + K f P + F 1 = 0,
0.5 阻尼矩阵，K f 为流体等效刚度矩阵，P 为流体节点
声压矩阵。
0
0 1000 2000 3000 4000 流体介质的波动也会对结构形成作用，其结构
ᮠဋ/Hz
动力方程为
(b) ྲढ़ག2ៈ־ऄᮠ៨
¨
˙
M s U + C s U + K s U = F s + F f , (10)
0.7
x வՔ
0.6 y வՔ 式 (10) 中：M s 为结构质量矩阵，C s 为机构阻尼矩
z வՔ 阵，K s 为结构刚度矩阵，F s 为结构外激励矩阵，U
ҫᤴए/(mSs -2 ) 0.4 为结构位移矩阵。
0.5
0.3
0.2 综合方程 (2) 和方程 (3)，得到结构与流体的耦
合离散化矩阵方程为
0.1
       
U
U
0 M s 0  ¨  C s 0  ˙ 
0 1000 2000 3000 4000   +  
P
P
ᮠဋ/Hz R M f  ¨ 0 C f  ˙ 
(c) ྲढ़ག3ៈ־ऄᮠ៨      
K s −R T    F s 
U
图 11 特征点谐响应频谱 +   = . (11)
P
Fig. 11 Characteristic point harmonic response spectrum R K f    0 