Page 67 - 《应用声学》2021年第2期

第 40 卷 第 2 期 田野等： 数控裁剪机切割刀壳体振动噪声预测分析 235

根据声压级计算公式
᫾ࡉ౜b
N dB = 20 lg M(ω), (12) ᫾ࡉ౜a

式(12) 中，M(ω) 为传递函数的增益，为频响函数与
参考值的比值，其中参考值为2 × 10 −5 Pa/N。
将图 10 中实验测得的数据进行数值计算转换
为声压级频谱曲线，并与声固耦合分析 100 mm 处
声压级计算结果进行对比，如图14所示。结果显示， ᫾ࡉ౜c
计算结果与实验结果曲线波形基本一致，均在固有
频率处产生的峰值；且实验结果 1、2、3 的均方根分
别为 80.93 dB(A)、77.79 dB(A)、87.31 dB(A)，计算
结果均方根为 77.06 dB(A)，差值较小，表明了计算
结果的可靠性。

140
ࠄᰎፇ౧1
ࠄᰎፇ౧2
120
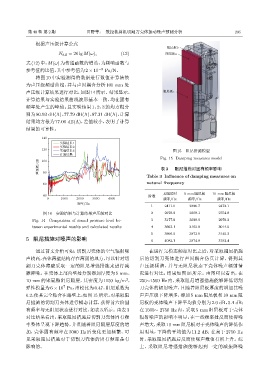
ࠄᰎፇ౧3 图 15 阻尼措施模型
ᝠካፇ౧
Fig. 15 Damping measures model
ܦԍጟ/dB 表 3 阻尼措施对固有频率影响
100
80
Table 3 Influence of damping measures on
60 natural frequency

无阻尼时 5 mm 阻尼板 10 mm 阻尼板
40 阶数
0 1000 2000 3000 4000 频率/Hz 频率/Hz 频率/Hz
ᮠဋ/Hz
1 2411.6 2396.7 2473.1
图 14 实验结果与计算结果声压级对比 2 2978.9 2908.1 2754.8
Fig. 14 Comparison of sound pressure level be- 3 3177.8 3098.9 2978.2
tween experimental results and calculated results 4 3662.1 3163.8 3014.0
5 3906.5 3873.9 3145.2
5 阻尼措施对噪声的影响 6 4082.1 3974.8 3192.4

通过前文分析可知，切割刀壳体的空气辐射噪 在进行完模态频率对比之后，对采取阻尼措施
声较高，壳体薄壁结构存在薄弱的地方，可以针对切 后的切割刀壳体进行声固耦合仿真计算，得到其
割刀壳体薄壁采取一定的阻尼增强措施来进行减 声压级频谱，并与无阻尼状态下壳体噪声辐射情
振降噪。在壳体上部内壁处分别添加厚度为 5 mm、 况进行对比，结果如图 16 所示。由图可以看出，在
3
10 mm 的聚氨酯阻尼隔层，其密度为 1150 kg/m ， 250∼1500 Hz 内，采取阻尼增强措施能够降低切割
7
弹性模量为 6 × 10 Pa，泊松比为 0.47，阻尼系数为 刀壳体的辐射噪声，且随着阻尼板厚度的增加其噪
0.2，使其完全贴合在薄壁上，如图15 所示。对采取阻 声声压级下降增多，添加 5 mm 阻尼板和 10 mm 阻
尼措施的切割刀壳体进行模态计算，获得前六阶固 尼板的壳体噪声下降平均值分别为2.6 dB、5.4 dB；
有频率与无阻尼状态进行对比，如表 3所示。由表 3 在 1500∼ 2750 Hz 内，采取 5 mm 阻尼板对于壳体
对比结果看出，采取阻尼措施后切割刀壳体固有频 辐射噪声的影响不明显，在一些频率处反而使得噪
率整体呈现下降趋势，并且随着阻尼隔层厚度的增 声增大，采取10 mm 阻尼板对于壳体噪声的降低作
加，壳体固有频率在 3000 Hz 后变化更加频繁，可 用明显，下降的平均值为 11.2 dB；在高于 2750 Hz
见采取阻尼措施对于切割刀壳体的固有频率是有 时，采取阻尼措施后反而使噪声数值有所上升。综
影响的。 上，采取阻尼增强措施能够起到一定的减振降噪