Page 92 - 《应用声学》2021年第2期

260 2021 年 3 月

分析原因认为，由分析域信号差异以及相似度 3.2 单频激励下，超声信号的相似度分析与反
函数所关注特征不同两点因素造成的。图15、图 16 射系数
分别给出了不同压力下时、频域信号局部图，对 作为对比，开展了单频激励下承压界面超声检
比发现，时、频域信号的相对幅值差异明显，时 测实验。实验中，激励信号为5周期汉宁窗调制正弦
域信号最大幅值约为 (0.5 V)，频域信号幅值约为 信号，其中心频率与换能器中心频率相同(2 MHz)。
(2.5 × 10 −3 )；随着外载压力增加，时域幅值的相对 图17、图18给出了两种激励模式下2.5 MPa下典型
变化远大于频域幅值的相对变化。 信号，可以看出，宽频激励下时频域信号的强度均好
0.5 于单频激励下结果，随着压力增加，时域信号的差异
0.5 MPa 也更明显。
1.0 MPa
1.5 MPa
2.0 MPa 0.5
2.5 MPa ࠕᮠ༏ҵ
ӭᮠ༏ҵ
ႃԍ/V 0

ႃԍ/V 0

-0.5
17.0 17.5 18.0 18.5
௑ᫎ/µs

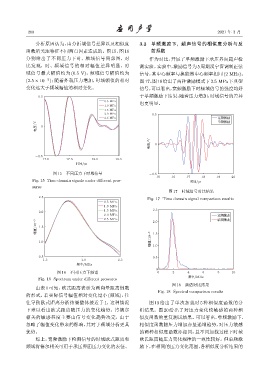
图 15 不同压力下时域信号 -0.5
15 16 17 18 19 20
Fig. 15 Time domain signals under different pres- ௑ᫎ/µs
sures
图 17 时域信号对比结果
2.5
Fig. 17 Time domain signal comparison results
0.5 MPa
1.0 MPa
1.5 MPa 2.5
2.0
2.0 MPa ࠕᮠ༏ҵ
2.5 MPa 2.0 ӭᮠ༏ҵ
ࣨϙ/10 -3 1.5 1.5
ࣨϙ/10 -3
1.0 1.0

0.5 0.5
1.5 2.0 2.5
ᮠဋ/MHz
0
图 16 不同压力下频谱 0 2 4 6 8 10
ᮠဋ/MHz
Fig. 16 Spectrum under different pressures
图 18 频谱对比结果
由表 1 可知，欧式距离表示为两向量距离倒数
Fig. 18 Spectral comparison results
的形式，若实际信号幅值相对变化过小 (频域)，往
往导致欧式距离分析结果整体接近于 1，这种情况 图 19 给出了单次加载时 5 种相似度函数的分
下难以看出欧式距离随压力的变化趋势。肯德尔 析结果。图 20 给出了对压力变化较敏感的两种相
相关的敏感程度主要由信号变化趋势决定，由于 似度函数的重复测试结果。可以看出，单频激励下，
忽略了幅值变化带来的影响，其对于频域分析更具 相似度函数随压力增加亦呈递增趋势，对压力敏感
优势。 的两种相似度函数亦相同，且不同加载过程下时域
综上，宽频激励下检测信号的时域欧式距离和 欧氏距离随压力变化规律的一致性较好。但单频激
频域肯德尔相关可用于承压界面压力变化的表征。 励下，在相同的压力变化范围，各相似度分析结果的