Page 59 - 《应用声学》2021年第4期

第 40 卷 第 4 期 蒋瑜等： 表征超声衰减谱粒度的改进和声搜索算法 543

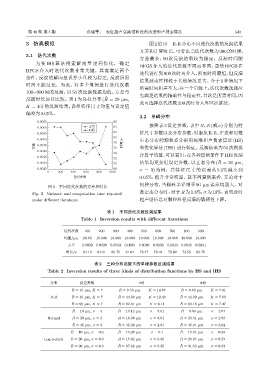
3 仿真模拟 图2给同一R-R分布不同迭代次数的反演结果

方差和计算时长，可看出当迭代次数为 200 的时候，
3.1 迭代次数
方差最小，50 次反演结果较为稳定。反演时间随
为使 IHS 算法搜索解向量过程优化， 确定
BFGS 介入的迭代次数不同而不同，显然 BFGS 在
BFGS 介入时迭代次数非常关键。其需满足两个
迭代进行到 900次时再介入，所需时间最短，但反演
条件：反演的解向量误差小且较为稳定；反演所需
结果波动性相较于其他情况更大。介于 9 种情况下
时间不能过长。为此，对多个算例进行迭代次数
所需时间相差不大，在一个量级上，迭代次数选择应
100∼900 间的反演，以 50 次反演数据均值、方差与
先满足结果的精确性与稳定性，其次是所需时间，因
¯
反演时长加以比较。表 1 为 R-R 分布 (R = 20 µm,
此可选择迭代次数200次时介入BFGS算法。
K = 10) 的反演结果，各组特征尺寸均值与设定值
偏差为0.05%。
3.2 单峰分布
0.0065 86
¯
0.0060 வࣀ 84 按照表 2 设定参数，表中 R、K(或 σ) 分别为特
௑ᫎ
0.0055 82 征尺寸参数以及分布参数，对服从R-R、正态和对数
80
0.0050 正态分布的颗粒系分别用标准和声搜索算法 (HS)
78 ௑ᫎ/s
வࣀ 0.0045 76 和优化算法(IHS) 进行验证。反演结果为50次模拟
0.0040
74 计算平均值，可以看出，在各种算例条件下IHS反演
0.0035 72
¯
0.0030 70 结果均更接近设定参数，以正态分布 (R = 20 µm,
0.0025 68 σ = 3) 为例，其特征尺寸的误差从 5.1% 减小到
0 200 400 600 800 1000
ᤖ̽൓஝ 0.05%，提升非常明显。就不同算例来看，无论对于
何种分布，当颗粒半径增至 90 µm 误差均最大。对
图 2 不同迭代次数的方差和时长
¯
Fig. 2 Variance and computation time required 数正态分布时，对于 R 为 1.8%，σ 为 10%，表明此时
under different iterations 超声谱信息对颗粒粒径反演的敏感性下降。

表 1 不同迭代次数反演结果
Table 1 Inversion results with different iterations

迭代次数 100 200 300 400 500 600 700 800 900
均值/µm 19.99 19.998 19.998 19.998 19.998 19.998 19.998 19.998 19.997
方差 0.0039 0.0029 0.0032 0.0035 0.0040 0.0038 0.0043 0.0045 0.0061
时长/s 84.12 84.01 80.75 81.64 78.47 78.44 78.02 73.55 69.75

表 2 三种分布函数下的单峰参数反演结果
Table 2 Inversion results of three kinds of distribution functions by HS and IHS

分布 设定参数 HS IHS
¯
¯
¯
R = 10 µm, K = 7 R = 9.56 µm K = 14.87 R = 9.99 µm K = 7.61
¯
¯
¯
R-R R = 45 µm, K = 7 R = 44.08 µm K = 12.40 R = 44.99 µm K = 7.00
¯
¯
¯
R = 90 µm, K = 7 R = 92.91 µm K = 6.11 R = 89.16 µm K = 7.47
¯
¯
¯
R = 10 µm, σ = 3 R = 10.12 µm σ = 3.61 R = 9.99 µm σ = 2.97
¯
¯
¯
Normal R = 20 µm, σ = 3 R = 18.98 µm σ = 3.64 R = 20.01 µm σ = 2.99
¯
¯
¯
R = 45 µm, σ = 3 R = 45.38 µm σ = 2.64 R = 45.01 µm σ = 3.02
¯
¯
¯
R = 10 µm, σ = 0.3 R = 10.28 µm σ = 0.1 R = 10.01 µm σ = 0.29
¯
¯
¯
Log-normal R = 20 µm, σ = 0.3 R = 17.82 µm σ = 0.36 R = 20.87 µm σ = 0.27
¯
¯
¯
R = 90 µm, σ = 0.3 R = 97.02 µm σ = 0.35 R = 91.63 µm σ = 0.33