Page 60 - 《应用声学》2021年第4期

544 2021 年 7 月

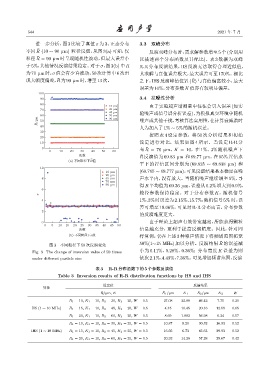
进一步分析，图 3 比较了真值 σ 为 3、正态分布 3.3 双峰分布
¯
不同 R (10 ∼ 90 µm) 粒径反演，从图 3(a) 可知，仅 反演双峰分布时，需求解参数增至 5个(分别用
¯
粒径 R = 90 µm 时呈现随机性波动，但最大误差小 以描述两个分布函数及其配比)。表 3 数据为双峰
¯
于5%，其他情况反演结果稳定。对于σ，图3(b)中R R-R 分布反演结果，HS 反演无法取得合理近似值，
为70 µm 时，σ 值会有少许波动，50次计算中6 次出 其求解与真值误差极大，最大误差可至 170%。相比
¯
现大幅度偏差，R 为90 µm时，增至13次。 之下，IHS 反演峰值位置 (R) 与真值偏离较小，最大
¯
误差为10%，分布参数K 值亦有较明显偏差。
100
90 3.4 抗噪性分析
80
10 µm 由于实验超声谱测量中往往会引入误差 (如实
70 20 µm
45 µm 验噪声或信号谱分析误差)，为模拟真实环境中随机
60 70 µm
R/µm 50 90 µm 噪声或其他干扰，考核算法实用性，在计算衰减谱时
40
人为加入了1% ∼ 5%的随机误差。
30
按照表 4 设定参数，将 50 次分析结果和初始
20
10 设定进行对比，结果如图 4 所示。当设定 R-R 分
¯
0 布 R = 70 µm、K = 10，在 1%、3% 随机噪声下
0 10 20 30 40 50 60
൓஝ R 反演值为 69.83 µm 和 69.77 µm，在 95% 置信水
¯
(a) ˀՏዢय़ʾRϙ
平下的置信区间分别为 (69.825 ∼ 69.838 µm) 和
10
10 µm (69.765 ∼ 69.777 µm)，可见反演结果基本稳定在噪
20 µm
8 45 µm 声水平内，没有放大。当随机噪声继续增至 5%，寻
70 µm
¯
90 µm 得 R 平均值为 69.36 µm，误差从 0.2% 增大到 0.9%，
6
粒径参数保持稳定。对于分布参数 K，随机信号
σ
4 1%、3%时误差为2.15%、15.7%，随机信号5% 时，误
差可增至 19.66%，可见对 R-R 分布而言，分布参数
2
的反演难度更大。
0 由于理论上超声有效带宽越宽，所能获得颗粒
0 5 10 15 20 25 30 35 40 45 50
൓஝ 信息越充分，更利于提高反演精度。因此，针对同
(b) ˀՏዢय़ʾσϙ 样算例，仍在上述 3 种噪声情况下将频谱范围拓宽
¯
图 3 不同粒径下 50 次反演变化 50%(1∼15 MHz) 加以分析。反演结果 R 的误差减
Fig. 3 The change of inversion value of 50 times 小为 0.11%、0.28%、0.36%；分布宽度 K 误差为则
under different particle size 依次2.1%、4.49%，7.36%。可见增加频谱范围，反演

表 3 R-R 分布函数下的 5 个参数反演值
Table 3 Inversion results of R-R distribution functions by HS and IHS
设定值 反演结果
算法
¯
¯
¯
R/µm, K R 1 /µm K 1 R 2 /µm K 2 W
¯
¯
R 1 = 10, K 1 = 10, R 2 = 30, K 2 = 25, W = 0.5 27.08 22.98 46.42 7.75 0.20
¯
¯
HS (1 ∼ 10 MHz) R 1 = 15, K 1 = 10, R 2 = 45, K 2 = 25, W = 0.5 4.75 10.45 20.16 12.55 0.65
¯
¯
R 1 = 20, K 1 = 10, R 2 = 60, K 2 = 25, W = 0.5 8.69 1.892 56.98 6.24 0.57
¯
¯
R 1 = 10, K 1 = 10, R 2 = 30, K 2 = 25, W = 0.5 10.87 8.20 30.32 16.93 0.52
¯
¯
IHS (1 ∼ 10 MHz) R 1 = 15, K 1 = 10, R 2 = 45, K 2 = 25, W = 0.5 16.66 6.73 45.63 29.93 0.52
¯
¯
R 1 = 20, K 1 = 10, R 2 = 60, K 2 = 25, W = 0.5 20.92 14.26 57.28 29.67 0.42