Page 76 - 《应用声学》2021年第5期

720 2021 年 9 月

11 (对应 11 类特征)，即 X s ∈ R ，Y s ∈ {−1, +1}， 曲线上会标记一个与曲线同色的实心点，该点表示
11
“−1” 代表杂波，“+1” 代表目标，为少数类样本。在 决策门限值为 0.5 时，算法能够达到的检测概率和
该数据集上做 10 次 3 折交叉验证 [13] ，即每一次交 虚警概率。为了使得算法输出结果具有一定的统
叉验证前分别将杂波和目标样本随机等分为 3 份 计意义和可信度，本文将机器学习算法的输出通过
(每一份称为一折)，即 Data1、Data2 和 Data3，如 Sigmoid 函数统一映射为正样本 (目标) 的后验概率
表 2 所示，并形成 3 组训练集和测试集：(1) 训练集 值，即未知样本数据是目标的可能性，后验概率值
Data1 + Data2，测试集Data3；(2) 训练集Data1 + 越大，是目标的可能性越大。对于一条ROC性能曲
Data3，测试集 Data2；(3) 训练集 Data2 + Data3， 线，当取不同的后验概率值作为决策门限时，该门
测试集Data1。 限将对应一组不同的检测概率和虚警概率，为了防
分别在 (1)、(2) 和 (3) 上训练并测试，重复进行 止人为的先验知识对结果产生干扰，同时，为了使
10次，以减小实验过程中的随机性。 得不同算法具有相同的衡量标准，本文选取了概率
值为 0.5 处作为决策门限，大于 0.5，则该未知样本
表 2 水声目标 -杂波样本
数据就是目标，否则是杂波，实现了从统计意义上
Table 2 Underwater acoustic target-clutter
的可能性向确定性决策的转变。Auc值说明了ROC
sample
性能曲线接近左上角的程度，而实心点处对应的检
测概率和虚警概率则进一步说明了算法在统计意
Data1 Data2 Data3 总计
义上的优劣。
杂波数 8586 8586 8586 25758
目标数 35 35 35 105
1.0
总计 8621 8621 8621 25863
0.9
3.3 实验结果及分析
为便于比较，标准 SVM、CS-SVM 和本文算 ೝ฾ഐဋ 0.8
法 En-SVM 均采用径向基核函数，核自由参数 δ 取 0.7
1，采用序列最小最优化 (Sequential minimal opti-
Auc=0.97 En-SVM
mization, SMO) 算法，由于涉及样本间距离的计 0.6 Auc=0.94 CS-SVM
Auc=0.85 SVM
算，为防止受到具有过高特征值或过低特征值样
0.5
0 0.2 0.4 0.6 0.8 1.0
本的影响，输入数据均做标准化处理。CS-SVM 和 ᘿ᝝ഐဋ
En-SVM 中的假负例 FN 与假正例 FP 的代价之比
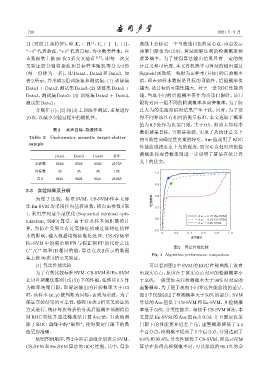
图 2 算法性能比较
C /C 取和 IR 相同的值，算法在表 2 所示的数据
+
−
Fig. 2 Algorithm performance comparison
集上做10次3折交叉验证。
(1) 算法性能比较 可以看到图 2 中SVM的ROC性能曲线上没有
为了有效比较标准 SVM、CS-SVM 和En-SVM 出现实心点，原因在于其实心点对应的检测概率小
在贝叶斯最优准则 (式(5)) 下的性能，始终以0.5 作 于 50%，一般更加关注检测概率大于 90% 时对应的
为概率决策门限，即算法输出的后验概率大于 0.5 虚警概率，为了便于观察不同算法性能曲线的差异，
时，该样本 (x, y) 被判断为目标，否则为杂波。为了 图2中仅绘制出了检测概率大于50%的部分。SVM
保证实验结果的可靠性，按照 10 次 3 折交叉验证的 算法的 Auc 值低于 CS-SVM 和 En-SVM，且检测概
方式进行，统计每次每折的分类后验概率预测值绘 率低于50%，分类性能差。相较于 CS-SVM算法，本
制 ROC 曲线并通过梯度法计算 Auc 值，有效地消 文算法 En-SVM 的 Auc 值高出 0.03，并且固定决策
除了 ROC 曲线中的 “锯齿”，使得固定门限下的数 门限下的性能更靠近左上角，虚警概率降低了 3.4
值更加准确。 个百分点，检测概率提高了 5 个百分点，分别达到了
依照图例顺序，图2中所示曲线分别表示SVM、 9.9%和95.6%，分类性能优于CS-SVM，即En-SVM
CS-SVM 和 En-SVM 算法的 ROC 性能，其中，每条 算法在获得高检测概率时，可以排除约 90.1% 的杂