Page 28 - 《应用声学》2021年第6期

824 2021 年 11 月

选取的块下标 U i ，并在扩充支撑原子下标集 M 后， 减系数和海底声衰减系数分别设为 α w = 0 dB/λ
重新计算对应导向矢量所张成超平面 A M 的投影矩 和α b = 0.1 dB/λ。仿真分析频率取 f = 100 Hz，使
( ) −1
H
H A ，最后更新残差向量 [12]
= A M A A M 用 Kraken 程序 计算波导模态，得到 4 阶简正模
阵P A M M M
r 和相对误差 ε。算法收敛后，输出下标序列 U 对应 深度函数。
的方位即估计的声源方位，拟合贡献系数 h 表示对
应声源方位的强度，作为BOMP的波束输出，ε为最 2.1 两个点声源的时间方位历程图
终的拟合相对误差。 仿真两个点声源同时做 5 m/s水平匀速直线运
动，运动轨迹如图3所示。声源深度均为5.7 m，源谱
2 数值仿真
S i (f = 100 Hz)幅度均设为1，由于声源运动速度相

根据 2011 年北黄海声学实验中一次实测的声 对水介质中声速很小，所以不考虑多普勒频移效应。
速剖面，并以介质均匀无限大液态海底作为仿真 同时接收阵元信噪比固定设为 20 dB，即不随声源
波导模型，如图 2 所示。水介质中声速接近等声速 位置变化，根据图 2 波导环境参数，仿真计算海底
c = 1480 m/s，海底声速设为 c b = 1650 m/s，海底 HLA接收声场信号，HLA孔径设为 1 km，均匀阵元
深度设为 H = 69 m，水介质密度和海底密度分别 间隔 5 m，阵元个数为 201 个，使用 CBF 和 BOMP
3
3
设为 ρ w = 1 g/cm 和 ρ b = 1.8 g/cm ，水介质声衰 方法分别进行声源的方位历程估计，结果如图4(a)、

5.7 m c  =1479.6 m/s
 ρ w=1 g/cm 3
ງए/m  α w=0 dB/λ വগງएѦ஝

 c  /⊲ m/s
H=69 m
c b=1650 m/s ρ b=1.8 g/cm 3 α b=0.1 dB/λ

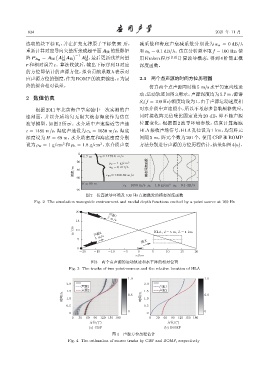
图 2 仿真波导环境及 100 Hz 点源激发的模态深度函数
Fig. 2 The simulation waveguide environment and modal depth functions excited by a point source at 100 Hz

20 ܦູ1

15 5 m/s
y/km 10 ܦູ2 HLA, d=5 m, L=1 km

5 5 m/s
ஊܸ
0
-20 -15 -10 -5 0 5 10 15 20
x/km
图 3 两个点声源的运动轨迹和水平阵的相对位置
Fig. 3 The tracks of two point-sources and the relative location of HLA

1.0 1.0
2.0 2.0
ܦູ1 ܦູ1
1.5 ܦູ2 ܦູ2
௑ᫎ/h 1.0 0.5 ௑ᫎ/h 1.5 0.5
1.0
0.5 0.5
0 0
0 0
0 30 60 90 120 150 180 0 30 60 90 120 150 180
வͯ/(O) வͯ/(O)
(a) CBF (b) BOMP
图 4 声源方位历程估计
Fig. 4 The estimation of source tracks by CBF and BOMP, respectively