Page 48 - 《应用声学》2022年第1期

44 2022 年 1 月

130 频谱上存在 131 Hz 的峰值，这是列车以 300 km/h
ᣁՔ౶ӝ۫٪ܦ 583 714 844 的速度运行于轨枕间距为 0.625 m 的线路上而产
120
ܦԍጟ/dB(A) 110 132 生的过轨枕冲击导致的。因此，初步推测导致非
451
100
90
80
70 圆化磨耗激励频率两侧出现轮轨噪声边频带的
原因或许和过轨枕冲击有关。为了进一步开展转
10 1
向架区域噪声边频带产生机理的研究，需要借助
૝үҫᤴए/g 10 -1 理论计算。
0
10
45
-2
10
10 -3 ᣉኸ૝ү 35 ᪮Ց0 km 4
᪮Ց8f10 km
0 200 400 600 800 1000 1200 ᪮Ց14f10 km
4
ᮠဋ/Hz 25 ᪮Ց18f10 km
4
图 3 振动噪声频谱特性对比 15
Fig. 3 Spectrum of the sound pressure level of ዤጀएඵࣱ/dB(ref=1 µm)
bogie region and the acceleration of axlebox 5
影响轮轨噪声的主要因素为轮轨表面粗糙度 -5
水平，由于在测试之前，对运行区间的钢轨进行了 -15
打磨，所以认为钢轨表面状态良好，故需要重点关 -25
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30
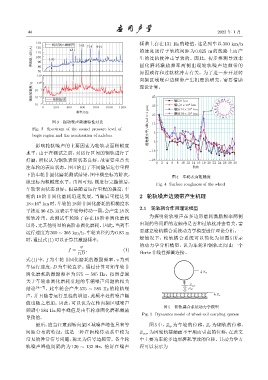
注车轮的表面状态。图4 给出了不同镟后运行里程 ᫽൓
下的车轮非圆化磨耗测试结果，图中横坐标为阶次，
图 4 车轮表面粗糙度
纵坐标为粗糙度水平。由图可知，刚进行完镟修后，
Fig. 4 Surface roughness of the wheel
车轮表面状态良好。但是随着运行里程的提高，车
轮的 18 阶非圆化磨耗迅速发展，当镟后里程达到 2 轮轨噪声边频带产生机理
4
18×10 km时，车轮的 18阶非圆化磨耗的粗糙度水
2.1 轮轨耦合作用理论模型
平接近30 dB，这表示车轮每转动一圈，会产生18次
轮轨冲击。此测试车轮除了存在 18 阶非圆化磨耗 为探明轮轨噪声在多边形磨耗激励频率两侧
以外，无其他明显的高阶非圆化磨耗。因此，当列车 出现的等间距的边频带是否和过轨枕冲击有关，需
运行速度为 300 ∼ 305 km/h、车轮直径约为0.83 m 要建立轮轨耦合系统动力学模型进行理论分析。一
时，通过式(1)可以计算其激励频率： 般情况下，轮轨耦合系统可以简化为如图 5 所示
v 的动力学分析模型，认为车轮和钢轨之间由一个
f = , (1)
πD Hertz非线性弹簧连接。
式 (1) 中，f 为车轮非圆化磨耗的激励频率，v 为列
车运行速度，D 为车轮直径。通过计算可知车轮非
圆化磨耗的激励频率为 575 ∼ 585 Hz。按照普遍 Z w
关于车轮非圆化磨耗引起的车辆噪声问题的相关
Z oor
结论 [4−7] ，此车轮会产生 575 ∼ 585 Hz 的轮轨噪 P N
声，并且随着运行里程的增加，此频率处的噪声幅 Z r
值也随之增加。因此，可以认为在转向架区域噪声
图 5 轮轨耦合系统动力学模型
频谱中 584 Hz 频率峰值是由车轮非圆化磨耗激励
Fig. 5 Dynamics model of wheel-rail coupling system
导致的。
最后，应当注意到转向架区域噪声峰值具有等 图 5 中，Z w 为车轮的位移，Z r 为钢轨的位移，
间距分布的特征，这是一种在齿轮传动系中较为 Z oor 为因轮轨接触面不平顺而引起的位移，在此文
常见的异常信号问题，称之为信号边频带。各个轮 中主要为车轮多边形磨耗导致的位移。其动力学方
轨噪声峰值间隔约为 130 ∼ 132 Hz，恰好在噪声 程可以表示为