Page 50 - 《应用声学》2022年第1期
P. 50
46 2022 年 1 月
ࣨϙ/kN ࣨϙ/kN
0 200 400 600 800 1000 1200 1400 1600 0 200 400 600 800 1000 1200 1400 1600
ᮠဋ/Hz ᮠဋ/Hz
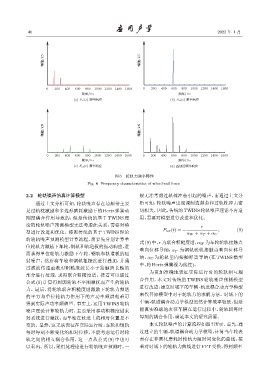
(a) F s ↼t↽ ᮠဋ־ऄ (b) F s ↼t↽ ᮠဋ־ऄ
ࣨϙ/kN ࣨϙ/kN
0 200 400 600 800 1000 1200 1400 1600 0 200 400 600 800 1000 1200 1400 1600
ᮠဋ/Hz ᮠဋ/Hz
(c) F s ↼t↽ ᮠဋ־ऄ (d) ԯҫՑᮠဋ־ऄ
图 6 轮轨力频率特性
Fig. 6 Frequency characteristics of wheel-rail force
2.2 轮轨噪声仿真计算模型 般无法考虑过轨枕冲击引起的噪声,而通过上文分
通过上文分析可知,轮轨噪声存在边频带主要 析可知,轮轨噪声出现调制边频带和过轨枕冲击密
是过轨枕激励和多边形磨耗激励下的 Hertz 弹簧动 切相关。因此,传统的TWINS轮轨噪声理论不再适
刚度耦合作用导致的,但是传统的基于 TWINS 理 用,需要对模型进行改进和优化。
论的轮轨噪声预测模型无法考虑此关系,需要对模 r
型进行改进和优化。按照传统的基于 TWINS 理论 F wr (t) = − α W + α T + α C , (9)
的轮轨噪声预测模型计算流程,需要先分别计算单
式(9)中,r 为联合粗糙度谱,α W 为车轮轮轨接触点
位轮轨力激励下车轮、钢轨和轨道板的振动响应,进
垂向位移导纳,α T 为钢轨轮轨接触点垂向位移导
而求得单位轮轨力激励下车轮、钢轨和轨道板的辐
纳,α C 为轮轨垂向接触弹簧导纳 (在 TWINS 模型
射噪声。然后将车轮和钢轨粗糙度进行叠加,并通
中,将Hertz弹簧视为线性)。
过滤波传递函数对粗糙度波长小于接触斑长轴的
为更加准确地表征实际运行时的轮轨相互耦
部分进行处理,求得联合粗糙度谱。接着可以通过
合作用,本文对传统的 TWINS 轮轨噪声预测模型
公式 (9) 计算得到因轮轨不平顺激扰而产生的轮轨
进行改进,建立时域下的车辆-轨道耦合动力学模型
力。最后,将轮轨联合粗糙度谱激励下轮轨力频谱
的平方与单位轮轨力作用下的声功率频谱相乘可 来代替原模型中对于轮轨力的求解方法。时域下的
得到实际声功率频谱 [9] 。事实上,运用TWINS轮轨 车辆-轨道耦合动力学模型虽然计算效率较低,但是
噪声理论计算轮轨力时,主要采用移动粗糙度谱来 能真实准确地表征车辆在运行过程中,轮轨间每时
对系统进行激扰,而车轮在轨道上的相对位置是不 每刻的耦合作用,满足本文的研究需要。
变的。显然,这无法表征在实际运行时,车轮和钢轨 本文轮轨噪声的计算流程如图7所示。首先,通
每时每刻不断变化的相对位移,不能考虑运行时轮 过建立的车辆-轨道耦合动力学模型,计算当车轮表
轨之间的相互耦合作用,这一点从公式 (9) 中也可 面存在非圆化磨耗时轮轨力随时间变化的曲线,接
以看出。所以,采用此理论进行轮轨噪声预测时,一 着对时域下的轮轨力曲线进行FFT变换,得到频率