Page 78 - 《应用声学》2022年第5期

754 2022 年 9 月

 使用前文中描述的 AP 方法进行波束分离的过

◦
 程如图6所示。从图6(a)可以看出，波束1接近5.5 ，
从接收信号中消除波束 1 后，重新搜索波束最大值，

找到波束 2 为 −9 ，即为图 6(b) 所示；同理，消除波
◦

束1和波束 2 后波束 3 在13 ，消除波束1、2、3 后，波
◦
 束4在19 ，结果如图6(c)和图6(d)所示。
◦
ງए/m  1.0
0.5 1
 0
-30 -20 -10 0 10 20 30
 ᝈए/(O)
(a) ࡍᦊతܸϙฉౌ1
 1.0
2
0.5
 0
-30 -20 -10 0 10 20 30
 ᝈए/(O)
        (b) ࡍᦊతܸϙฉౌ2
ܦᤴ/(mSs -1 ) 1.0 3
100 ࣨए (ॆʷӑ) 0.5
Ctop=1572.3 m/s 0
ρ =1760 kg/m 3 -30 -20 -10 0 10 20 30
b
α =0.2 dB/λ ᝈए/(O)
Cbottom=1593.0 m/s
b
123 (c) ࡍᦊతܸϙฉౌ3
1.0
4
图 4 海洋环境模型 0.5
0
Fig. 4 Marine environmental model -30 -20 -10 0 10 20 30
ᝈए/(O)
(d) ࡍᦊతܸϙฉౌ4
使用置于上述波导环境中的 25 元垂直均匀线 1.0
阵，阵元间距为 1 m。布放在 38 ∼ 62 m 水深处。仿 0.5
0
真声源信号为 400 ∼ 1200 Hz 的宽带噪声信号。目 -30 -20 -10 0 10 20 30
ᝈए/(O)
标声源距离阵列中心的距离分别为 1600 m。带内 (e) ฉౌѬሏՑ
信噪比为20 dB。 图 6 利用 AP 方法进行波束分离
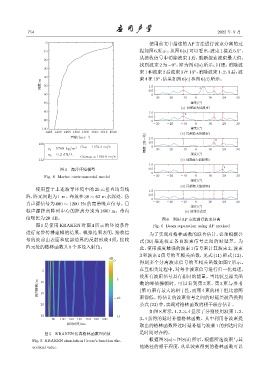
图 5 是使用 KRAKEN 对图 4 所示的环境条件 Fig. 6 Beam separation using AP method
进行宽带传播建模的结果。模拟结果表明，接收信 为了实现对格林函数的联合估计，必须根据公
号的波前由表面和底部边界的反射形成 4 组，接收 式 (20) 描述校正各自波束信号之间的时延差。为
阵元处的格林函数共8个多径入射角。 此，使用强度最强的波束 1 信号来计算波束 2、波束
3 和波束 4 信号的互相关函数，见式 (11) 和式 (12)。
dB
0
得到多个分离波束信号的互相关函数如图 7 所示。
在互相关过程中，对每个波束信号进行归一化处理，
5
使所有波束信号具有相同的能量。当比较互相关函
-5 数的峰值振幅时，可以看到第 2 束、第 3 束与参考
᫼ѵᡰሏ/m (第1) 束有最大的相干性，而第4束的相干性比前两
10
15
-10 束都低。将估计的波束信号之间的时延差被替换到
20 公式(23)中，实现对格林函数的相干联合估计。
如图8所示，1、2，3、4显示了分别使用波束1、2、
25 -15
80 100 120 140 160 180 200 3、4 获得的延时补偿格林函数。其中利用各波束提
ᄱࠫ௑ᫎ/ms 取出的格林函数经过时延补偿与波束 1 的到达时间

图 5 KRAKEN 仿真格林函数理论值 是时间对齐的。
Fig. 5 KRAKEN simulation Green’s function the- 根据图 8(a)∼ 图 8(d) 所示，根据所选波束与其
oretical value 他路径的相干程度，从单波束得到的格林函数可以