Page 25 - 《应用声学》2022年第6期

第 41 卷 第 6 期 陆悠南等： 应用于助听器反馈抑制的信噪比自适应滤波算法 871

NLMS 算法的复杂度过程中忽略了信噪比估计过 为了验证算法的反馈抑制性能，采用语声信号
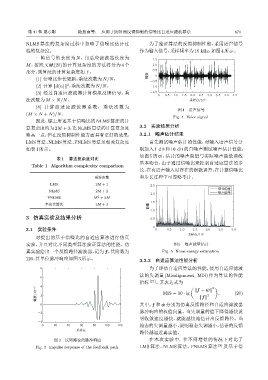
程的复杂度。 作为输入信号，采样频率为16 kHz，如图4所示。
一帧信号的长度为 N，自适应滤波器长度为 1.5
M，按照文献 [20] 的计算复杂度的方法将分为 4 个 1.0
部分，则算法的计算复杂度如下： 0.5
(1) 信噪比步长更新，乘法次数为N/N， ࣨए 0
-0.5
(2) 计算∥d(n)∥ ，乘法次数为N/N， -1.0
2
(3) 经过自适应滤波器计算模拟反馈信号，乘 -1.5
0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5
法次数为M × N/N， ᧔ನག/10 5
(4) 计算自适应滤波器系数， 乘法次数为
图 4 语声信号
(M × N + N)/N。
Fig. 4 Voice signal
因此，综上所述基于信噪比的 NLMS算法的计
算复杂度约为2M + 3，比NLMS算法的计算复杂度 3.2 实验结果分析
略高一点，但在反馈抑制性能方面具有更好的效果， 3.2.1 噪声估计结果
LMS算法、NLMS算法、PNLMS算法及相关复杂度 首先测试噪声估计的性能，对输入语声信号分
如表1所示。 别加入 1 dB 和 10 dB 的白噪声测试噪声估计性能，
如图 5 所示，估计的噪声能量与实际噪声能量曲线
表 1 算法复杂度对比
基本吻合，由于通过信噪比来控制自适应算法的步
Table 1 Algorithm complexity comparison
长，在有语声输入时存在的细微误差，在计算信噪比

乘法次数 和步长过程中可忽略不计。
LMS 2M + 1 2.5
ηՂᑟ᧚
NLMS 2M + 2 ٪ܦᑟ᧚
2.0
2
PNLMS M + 2M
1.5
本论文算法 2M + 3
ᑟ᧚
1.0
3 仿真实验及结果分析 0.5
0
3.1 实验条件 0 0.5 1.0 1.5 2.0 2.5 3.0
᧔ನག/10 5
对提出的基于信噪比的自适应算法进行仿真
实验，并且对比不同类型算法验证算法的性能。仿 图 5 噪声能量估计
真实验给出一个反馈路径滤波器，记为f，其阶数为 Fig. 5 Noise energy estimation
120，其单位脉冲响应如图3所示。 3.2.2 自适应算法性能分析

为了评估自适应算法的性能，使用自适应滤波
8
法的失调量 (Misalignment, MIS) 作为算法的性能
6
指标 [21] 。其表达式为
4 ( 2 )
ࣨए/10 -3 2 MIS = 10 · lg ∥f − ˆ w∥ , (20)
2
∥f∥
其中，f 和 ˆ w 分别为仿真反馈路径和自适应滤波器
0
脉冲响应的权值向量。当失调量的值下降得越快说
-2
明收敛速度越快，就能越快地估计出反馈路径。当
-4
0 20 40 60 80 100 120 稳态的失调量越小，说明稳态失调越小，估计的反馈
᧔ನག
路径越逼近真实值。
图 3 反馈路径的脉冲响应 在本次实验中，在不同增益的情况下对比了
Fig. 3 Impulse response of the feedback path LMS 算法、NLMS 算法、PNLMS 算法 [9] 及基于信