Page 26 - 《应用声学》2022年第6期

872 2022 年 11 月

噪比的 NLMS 算法，4 种算法的参数取相近收敛速 PNLMS、LMS、基于信噪比的NLMS算法。图7为4
度的情况下观测系统的失调性能，算法的复杂度由 种算法在稳态范围的失调量，可明显看出基于信噪
小到大按顺序分别为 LMS 算法、NLMS 算法、基于 比的 NLMS 算法的稳态失调量具有一定的优势，不
信噪比的 NLMS 算法、PNLMS 算法。4 种算法的步 仅具有更低的平均稳态失调量，同时稳态失调量的
长更新公式及参数取值如表2所示。 动态范围也更小。同时，本文提出的算法更多的是
取表 1 参数值，当增益为 36.9 dB 时，不同算法 对有语声信号时的失调量起伏范围具有参考意义，
的失调量如图6所示。 在信噪比低的时候其性能是和 NLMS 算法接近的，
而在信噪比高的时候，观察图 6 可明显发现其他算
0
法在语声出现时都会出现高的失调量，而本文算法
在语声出现时减小了语声相关性引起的失调量增
-5 大问题，提升了算法的性能。
ܿូ᧚/dB -10 0

NLMSካข
-15 LMSካข LMSካข
NLMSካข -5 PNLMSካข
PNLMSካข వ᝷஡ካข
వ᝷஡ካข
-20
0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 ܿូ᧚/dB -10
᧔ನག/10 5
-15
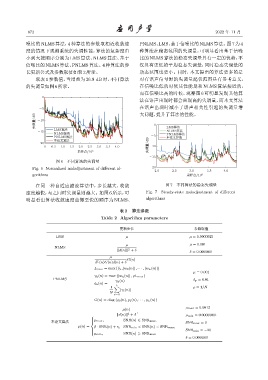
图 6 不同算法的失调量
Fig. 6 Normalized maladjustment of different al- -20
2.0 2.5 3.0 3.5 4.0
gorithms ᧔ನག/10 5

在同一种自适应滤波算法中，步长越大，收敛 图 7 不同算法的稳态失调量
速度越快，与之同时失调量则越大。如图 6 所示，可 Fig. 7 Steady-state maladjustment of different
明显看出算法收敛速度由慢至快的顺序为 NLMS、 algorithms

表 2 算法参数
Table 2 Algorithm parameters

更新步长 参数取值
LMS µ µ = 0.0000025
µ µ = 0.001
NLMS
2
∥d(n)∥ + δ
δ = 0.0000001
µ
G(n)
T
d (n)G(n)d(n) + δ
L max = max {δ p, |w 0 (n)| , · · · , |w L (n)|}
µ = 0.001
γ k (n) = max {|w k (n)| , ρL max}
PNLMS δ p = 0.01
γ k (n)
g k (n) =
L
1 ∑ ρ = 1/N
|γ i (n)|
N
i=0
G(n) = diag {g 0 (n), g 1 (n), · · · , g L (n)}
µ max = 0.0012
µ(n)
,
∥d(n)∥ + δ µ min = 0.00000001
2


本论文算法 µ max, SNR(n) 6 SNR min , SNR max = 0


µ(n) = β · SNR(n) + η, SNR min < SNR(n) < SNR max,
 SNR min = −20


µ min , SNR(n) > SNR max

δ = 0.0000001