Page 31 - 《应用声学》2022年第6期

第 41 卷 第 6 期 王亚琴等： 薄膜型声学超材料的结构设计与隔声特性 877

表 1 MAM 单胞尺寸参数 射、声波幅值为 1 Pa 的入射压力场以模拟声激励，
Table 1 Dimensional parameters of the 图中的下端面为声波出口，为无反射边界。当平面
MAM cell 波从声波入口处进入，遇到单胞后，一部分声波被反
射回去，一部分声波被局限于单胞内，还有一部分声
部件 参数/mm 值 部件 参数/mm 值
波透过单胞继续传播。
边长 a 100 臂长 cl 40
薄膜 米字摆臂 定义式 (1) 和式 (2) 两个积分算子，分别对声波
厚度 mh 0.2 宽度 cw 2
入口处和出口处的声压进行面积积分，可得入射声
半径 zr 6 边长 a 100
功率W in 和透射声功率W out ：
质量块 厚度 zh 2 框架 宽度 b 5
∫
至薄膜中心点 W in = P in dS in , (1)
35 厚度 h 2
距离 zp 2ρc
∫
P out
W out = dS out , (2)
表 2 MAM 单胞材料参数 [17] 2ρc
Table 2 Material parameters of the MAM 其中，P in 和 P out 分别表示入射声压和透射声压，ρ
cell [17] 和c分别表示空气的密度和声速，S in 和S out 分别表
示声波入口和出口端面的面积。
材料 密度 ρ/(kg·m ) 杨氏模量 E/P a 泊松比 µ
3
由此，结构或材料的隔声量，即STL可表达为
EVA 2050 1.7 × 10 8 0.45
PI 薄膜 1100 1.42 × 10 9 0.36 STL = 10 lg(W in /W out ). (3)
金属薄片 7800 2.0 × 10 11 0.33 相应地，薄膜入射方向上的法向平均位移d z 和
等效质量M eff 也可表示为式(4)和式(5)：
2 MAM单胞有限元模型构建
d z = ⟨w⟩ aveop , (4)
为研究所设计的米字摆臂多质量块 MAM 单 ∫ ∫
P in dS in − P out dS out
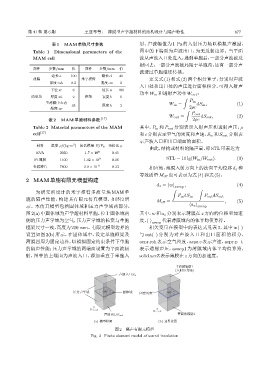
胞的隔声性能，构建其有限元仿真模型，如图 2 所 M eff = , (5)
示。本仿真模型包括固体域和压力声学域两部分， ⟨a z ⟩ aveop
图 2(a) 中固体域为声学超材料单胞，位于固体域两 其中，w 和 a z 分别表示薄膜在 z 方向的位移和加速
侧的压力声学域为空气，压力声学域的长宽与单胞 度，⟨ ⟩ aveop 代表薄膜域内的体平均值算符。
框架尺寸一致，高度为200 mm。有限元模型边界的 相关变量在模型中的表达式见表 3，其中 in( )
设置如图 2(b) 所示，在固体域中，设定单胞框架及 与 out( ) 分别为对声波入口和出口面积的积分，
薄膜四周为固定边界，以模拟固定约束条件下单胞 acpr.roh 表示空气密度，acpr.c 表示声速，acpr.p_t
的隔声性能；压力声学域的两端面设置为平面波辐 表示透射声压，aveop1 为薄膜域内体平均值算符，
射，图中的上端面为声波入口，添加垂直于单胞入 solid.accZ表示薄膜在z 方向的加速度。

ࣱ᭧ฉᣣ࠱1
(К࠱ԍҧڤ)
ܦฉК԰S in

ԍҧܦߦ۫ ڍʹ۫ ڍࠀጞౌ

z
y x y z x
ࣱ᭧ฉᣣ࠱2
ܦฉѣ԰S out
(a) വی಴౶ (b) ᣸ႍ᝺Ꮆ
图 2 隔声有限元模型
Fig. 2 Finite element model of sound insulation