Page 33 - 《应用声学》2022年第6期

第 41 卷 第 6 期 王亚琴等： 薄膜型声学超材料的结构设计与隔声特性 879

示，此时MAM单胞产生偶极型反谐振行为，入射声 3.0 3
d z
能在薄膜上的8 个质量块的平衡区域被充分抵消与 2.0 M eff 2
转移，整个单胞在入射声波与反射声波的共同作用 1
下处于准动态平衡状态，振动能量无法向前传播，从 1.0
而形成图 3 中 STL 曲线上的最大峰值 (对应频率点 ขՔࣱکͯረ d z/(10 -3 mm) 0 A  B  0 ኎஍᠏᧚ M eff/kg
B 0 )。 -1.0 -1

-2.0
-3
-3.0 -2
0 200 400 600 800 1000
ᮠဋ/Hz
(a) ߹டڏ

z 5.0 0.5
y x d z
ขՔࣱکͯረ d z/(10 -4 mm) 0 A  B  B  B  B  0 ኎஍᠏᧚ M eff/kg
(a) ኄ1᫽૝үവগ ̵f=94.8 Hz) M eff

z
y x A  A  A 
-5.0 -0.5
0 200 400 600 800 1000
(b) ኄ25᫽૝үവগ(f=590.5 Hz) ᮠဋ/Hz
(b) ࡍᦊஊܸڏ
图 4 MAM 单胞的两个典型振动模态
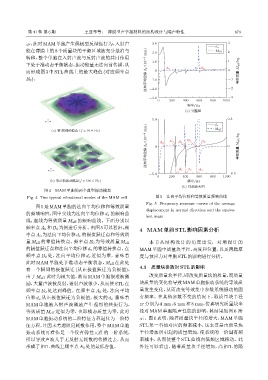
Fig. 4 Two typical vibrational modes of the MAM cell 图 5 法向平均位移和等效质量频响曲线
Fig. 5 Frequency response curves of the average
图 5 是 MAM 单胞的法向平均位移和等效质量
displacement in normal direction and the equiva-
的频域响应，图中实线为法向平均位移d z 的频响曲
lent mass
线，虚线为等效质量 M eff 的频响曲线。下面分别以
频率点A 0 和B 0 为例进行分析。由图5可以看出，频 4 MAM单胞STL影响因素分析
率点 A 0 为法向平均位移 d z 的极值跃迁点和等效质

量 M eff 的零值转换点，频率点 B 0 为等效质量 M eff 本节从结构设计的角度出发，对所设计的
的极值跃迁点和法向平均位移d z 的零值转换点。在 MAM单胞中质量块半径、高度和位置，以及薄膜厚
频率点 B 0 处，法向平均位移 d z 近似为零，意味着 度与预应力对单胞STL的影响进行分析。
此时 MAM 单胞处于准动态平衡状态，M eff 在此处
4.1 质量块参数对STL的影响
有一个瞬间的极值跃迁 (从正极值跃迁为负极值)，
由于 M eff 此时为极大值，故而 MAM单胞很难被激 改变质量块半径，即改变质量块的质量，而质量
励，大量声波被反射，透射声波很少，从而使 STL在 块质量的变化将导致MAM单胞振动系统的等效质
频率点 B 0 处达到峰值。在频率点 A 0 处，法向平均 量发生变化，从而改变等效集中参数系统振动的固
位移 d z 从正极值跃迁为负极值，极大的 d z 意味着 有频率。在其他参数不变的情况下，取质量块半径
MAM 单胞被入射声波激励产生强烈的共振行为， zr 分别为4 mm、6 mm和8 mm，仿真研究质量块半
等效质量 M eff 近似为零，也即模态质量为零，此时 径对 MAM 单胞隔声性能的影响，其结果如图 6 所
MAM单胞振动系统的二阶特征方程退化为一阶特 示。图 6 表明，随着质量块半径的增大，MAM 单胞
征方程，且因未考虑阻尼耗散作用，整个MAM单胞 STL 第一谷值对应的频率减小，这主要是由质量块
振动系统可看作是一个仅有弹性元件的一阶系统， 半径增加所引起的质量增加，使系统的一阶固有频
所以导致声波几乎无反射无耗散的传播过去，从而 率减小，从而使整个 STL 曲线向低频区域移动。此
形成了STL曲线上频率点A 0 处的最低谷值。 外还可以看出，随着质量块半径增加，高 STL 的隔