Page 32 - 《应用声学》2022年第6期

878 2022 年 11 月

表 3 相关变量表达式
Table 3 Expression of correlation variables

名称 表达式 单位 描述
w_in in((1[Pa]) 2/2/acpr.rho/acpr.c) W 入射声功率
w_out out(acpr.p_t 2/2/acpr.rho/acpr.c) W 透射声功率
STL 10*log10(w_in/w_out) 传声损失
dz -aveop1(w) m 法向 (z 向) 平均位移
F_in in(1[Pa]) N 入射端等效力
F_out out(acpr.p_t) N 透射端等效力
a_z -aveop1(solid.accZ) m/s 2 法向 (z 向) 加速度
M_eff (F_in-F_out)/a_z kg 等效质量

划分有限元模型的网格，设定自由四面体网格， 90 Hz，频率点 B 0 点处的 STL 最大，其所对应的频
选择用户控制网格划分，对最大和最小网格单元进 率为590 Hz。
行用户定义。声学分析时，最大网格单元尺寸不能
70
超过声速与最大分析频率比值的 1/6，当仿真最大 B 
频率 f max 为 1000 Hz 时，最大网格单元尺寸应不大 60
于c/(6 × f max ) = 56.7 mm。由于薄膜厚度较小，为 50 B  B 
尽可能保证计算精度，并兼顾计算时间，对薄膜采用 40
精细划分，取最小网络单元尺寸为 1.8 mm，其他各 ͜ܦ૯ܿ/dB A 
个域的最小网格单元尺寸为 3.6 mm。整个模型共 30
B 
20
被划分为 122619 个域单元、22818 个边界元和 1840
个边单元。 10 A 
A 
A 
0
3 MAM单胞隔声特性分析 0 100 200 300 400 500 600 700 800 900 1000
ᮠဋ/Hz
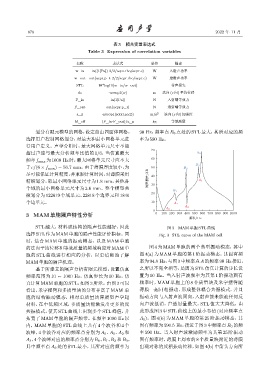
STL 越大，材料或结构的隔声性能越好，因此 图 3 MAM 单胞 STL 曲线
选择STL作为MAM单胞的隔声性能评价指标。同 Fig. 3 STL curve of the MAM cell
时，结合 MAM 单胞的振动模态，以及 MAM 单胞
的法向平均位移和等效质量的频域响应对MAM单 图 4 为 MAM 单胞的两个典型振动模态，其中
胞的 STL 曲线进行相应的分析，以更清晰地了解 图 4(a) 为 MAM 单胞的第 1 阶振动模态，其固有频
MAM单胞的隔声机理。 率为94.8 Hz，与图 3中频率点 A的频率90 Hz接近，
基于所建立的隔声分析有限元模型，设置仿真 之所以不完全相等，是因为 STL 仿真计算的步长设
频率范围为 10 ∼ 1000 Hz，仿真步长为 10 Hz，仿 置为 10 Hz。当入射声波频率为其第 1 阶振动固有
真计算 MAM单胞的 STL，如图3 所示。由图 3 可以 频率时，MAM 单胞上的 8 个质量块及米字摆臂随
看出，米字摆臂和多质量块的分布丰富了 MAM 单 薄膜一起同相振动，形成整体耦合共振模式，并且
胞的结构振动模态，相对单质量块薄膜型声学超 振动方向与入射声波同向，入射声能未能被任何反
材料，在中低频区域，多质量块能激发出更多的反 向声波抵消，声透射量最大，STL 值大大降低，由
共振模式，使其 STL 曲线上出现多个 STL 峰值，并 此形成图 3 中 STL 曲线上的最小谷值 (对应频率点
拓宽了 MAM 单胞的隔声频带。在频率 1000 Hz 以 A 0 )。图 4(b) 为 MAM 单胞的第 25 阶振动模态，其
内，MAM 单胞的 STL 曲线上共有 4 个波谷和 4 个 固有频率为 590.5 Hz，接近于图 3 中频率点 B 0 的频
波峰，4 个波谷对应的频率点分别为 A 0 、A 1 、A 2 和 率 590 Hz。当入射声波激励频率为其第 25 阶振动
A 3 ，4个波峰对应的频率点分别为B 0 、B 1 、B 2 和B 3 ， 固有频率时，薄膜上周布的 8 个质量块附近的薄膜
其中频率点 A 0 处的 STL 最小，其所对应的频率为 出现对称的反相振动位移，如图 4(b) 中箭头方向所