Page 134 - 《应用声学》2023年第2期

322 2023 年 3 月

B: modal B: modal
Total deformation 8 Total deformation 9
Type: Total deformation Type: Total deformation
Frequency: 90.944 Hz Frequency: 91.217 Hz
Unit: mm Unit: mm
2021/11/18 17:17 2021/11/18 17:20
19.609 max 19.994 max
18.341 18.706
17.074 17.417
15.806 16.129
14.538 14.841
13.270 13.552
12.002 12.264
10.735 10.976
9.4667 9.6874
8.1989 min 8.3991 min
y y
0 200.00 (mm) x 0 200.00 (mm) x
z z
100.00 100.00
(a) ូடՑᄊ኎஍ړဗ2Lവগ૝ی (b) ូடՑᄊ኎஍ړဗ2Hവগ૝ی
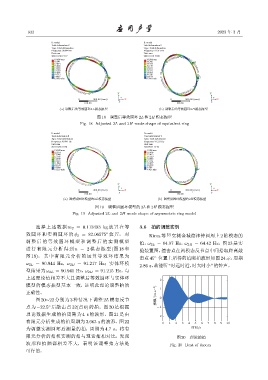
图 18 调整后等效圆环 2L 和 2H 模态振型
Fig. 18 Adjusted 2L and 2H mode shape of equivalent ring

B: modal B: modal
Total deformation 8 Total deformation 9
Type: Total deformation Type: Total deformation
Frequency: 90.941 Hz Frequency: 91.215 Hz
Unit: mm Unit: mm
2021/11/26 10:54 2022/2/25 12:34
19.588 max 19.98 max
18.314 18.696
17.040 17.413
15.766 16.129
14.492 14.845
13.218 13.561
11.944 12.277
10.570 10.993
9.3966 9.709
8.1227 min 8.425 min
y y
0 200.00 (mm) x 0 300.00 (mm) x
z z
100.00 150.00
(a) ូடՑړဗവیᄊ2Lവগ૝ی (b) ូடՑړဗവیᄊ2Hവগ૝ی
图 19 调整后圆环模型的 2L 和 2H 模态振型
Fig. 19 Adjusted 2L and 2H mode shape of asymmetric ring model

选择上述数据 m 2 = 0.113493 kg 放置在等 3.6 拍的调整实例
效圆环和实测圆环的 ϕ 2 = 82.06575 位置， 对 Kima 等 [9] 实测金城德神钟圆周上 2 阶模态的
◦
调 整 后 的 等 效 圆 环 模 型 和 调 整 后 的 实 测 模 型 拍，ω 2L = 64.07 Hz，ω 2H = 64.42 Hz，图 23 是实
进行有限元分析得到 n = 2 模态振型 (图 18 和 验装置图，撞击点在两模态反节点中间拾取距离敲
图 19)， 其中有限元分析的运算等效环结果为 击点 45 位置上所得的清晰拍波形如图 24示，周期
◦
ω 2L = 90.944 Hz，ω 2H = 91.217 Hz；实体环模
2.86 s，故能听“时远时近，时大时小”的钟声。
型结果为 ω 2L = 90.941 Hz，ω 2H = 91.215 Hz，与
上述理论值相差不大且调整后等效圆环与实体环
2
模型的模态振型基本一致，证明此理论调整拍的
正确性。 ૝ࣨ/(mSs -2 ) 1
图 20∼22 分别为 3 种情况下调整 2L 模态反节 0
点为 −22.5 后敲击点 32(点 0) 的拍。图 20 是根据 -1
◦
理论数据生成的拍周期为 4 s 的波形，图 21 是由 -2
有限元分析生成的拍周期为 3.663 s 的波形，图 22 0 1 2 3 4 5 6 7 8 9 10
为调整实测圆环后测量的拍，周期为 4.7 s。将有 ௑ᫎ/s
限元分析的拍和实测的拍与理论拍相对比，发现 图 20 理论的拍
波形和拍频都相差不大，表明该调整拍方法是 Fig. 20 Beat of theory
可行的。