Page 25 - 《应用声学》2023年第2期

第 42 卷 第 2 期 刘兢本等： 一种深度学习的立体阵波达方向估计方法 213

固定。目标方向在水平角和俯仰角 0 ∼180 范围 方位谱。
◦
◦
内采样，采样间隔 0.71 。数据处理时对不同时刻 观察图 13 的 0∼45 s 时间范围，目标船驶近实
◦
阵列接收信号计算二维方位谱。在谱峰方向沿着 验平台，接收信号功率由弱变强。在 0∼10 s 时间
水平角对二维方位谱横向切片，将不同时刻的水 范围内，本文方法比 CBF 方法目标轨迹显示更为
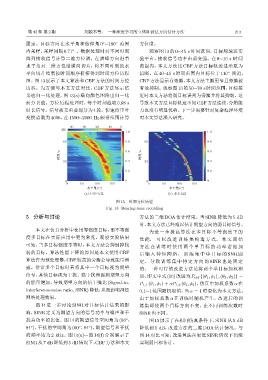
平向切片结果按时间顺序拼接得到时间方位历程 清晰。在 40~45 s 时间范围内目标位于 110 附近，
◦
图。图 13 展示了本文算法和 CBF 方法的时间方位 CBF 方法显示有旁瓣，本文方法主瓣更窄且旁瓣被
历程。为方便与本文方法对比，CBF 方法显示结 有效抑制。观察图 13 的 50∼70 s 时间范围，目标接
果也归一化处理，图 13(a) 横向颜色图给出归一化 近时本文方法将弱目标误判为旁瓣并将其抑制。这
前分贝值。方位历程处理时，每个时刻截取 0.68 s 导致本文方法目标轨迹不如CBF方法连续，分辨能
时长信号。信号被无重叠划分为 4 段。快速傅里叶 力也没有明显优势。下一步需要针对复杂海洋环境
变换点数为 4096，在 1500∼2000 Hz 频带范围计算 对本文算法深入研究。

-40 -30 -20 -10 0
dB
1.0 1.0
60 0.8 60 0.8

௑ᫎ/s 0.6 ௑ᫎ/s 0.6
30 0.4 30 0.4

0.2 0.2

0 0 0 0
0 50 100 150 0 50 100 150
ඵࣱᝈ/(°) ඵࣱᝈ/(°)
(a) CBFவข (b) వ஡வข
图 13 时间方位历程
Fig. 13 Bearing-time recording
5 分析与讨论 方法的二维 DOA 估计结果。当 SINR 降低为 5 dB

时，本文方法已经难以估计期望方向的弱目标信号。
本文在仿真分析中使用等强度目标，而不等强 为进一步提高算法在多目标不等强度下的
度多目标在实际应用中更为常见。观察实验结果 性 能， 可 以 改 进 训 练 集 构 造 方 式。 本 文 原 始
可知，当多目标强度不等时，本文方法会抑制掉较 方 法 在 训 练 时 使 用 两 个 单 目 标 的 功 率 谱 相 加
弱的目标。算法性能下降的原因是本文使用 CBF 后 输 入 神 经 网 络， 训 练 集 中 单 目 标 的 SNR 固
算法作为预处理器，CBF 较高的旁瓣会导致能量泄 定， 导 致 训 练集 中 特 定 方 向 的 SINR 也是 固 定
露。估计多个目标时若将其中一个目标视为期望 的。一种可行的改进方法是将两个单目标加权相
信号，其他目标视为干扰。强干扰泄露到期望方向 加，即文中式 (16) 改进为 P cbf {(θ 1 , ϕ 1 ) , (θ 2 , ϕ 2 )} =

的能量增加，导致期望方向的信干噪比 (Signal-to- P 1,1 (θ 1 , ϕ 1 ) + αP 1,2 (θ 2 , ϕ 2 )，仿真中加权系数 α 在
interference-noise ratio, SINR)降低，从而影响神经 0.1∼1 范围随机取值，当 α = 1 时退化为本文方法。
网络处理效果。 由于加权系数 α 在训练时随机产生，改进后的训
图 14 进一步讨论 SINR 对目标估计结果的影 练集即使两个目标方向不变，在不同训练次数时
响，SINR 定义为期望方向的信号功率与噪声和干 SINR也不同。
扰总功率的比值。图 14 的期望信号空间角为 (86 ， 图 15 展示了在相同仿真条件下，SINR 从 5 dB
◦
84 )，干扰的空间角为 (60 ，84 )，期望信号和干扰 降低到 1 dB，改进方法的二维 DOA 估计情况。与
◦
◦
◦
的频率均为 2 kHz。图 14(a)∼ 图 14(f) 分别展示了 图 14 对比可知，改进算法在更低 SINR 情况下仍能
SINR从7 dB降低到5 dB情况下，CBF方法和本文 实现弱目标估计。