Page 125 - 《应用声学》2023年第3期

第 42 卷 第 3 期 刘尧等： 道岔尖轨轨底缺陷的磁致伸缩导波监测实验研究 563

2
0.13 26 方程拟合确定系数为 R = 0.7488。由于监测过程
ᄣ฾௑ᫎ17:00-23:00
中的温度波动范围有限，虽然观察到参量 t A 与温度
22
ᑟ᧚ϙ/V 2 0.09 ພए/Ć 存在正相关性，但变化趋势尚难以用方程进行有效
拟合，后续不再做进一步分析。
18
3.2 温度补偿
9:00 —
0.05 14 采用基于标定方程和参考基准的两种温度补
0 10 20 30 40 50 60 70 80 90
ࠄᰎ൓஝
偿方法对导波监测信号进行处理。以缺陷反射回波
(a) Ԡ᧚E z
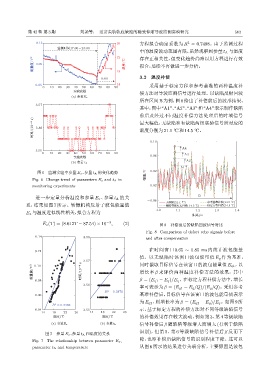
所在区间 B 为例，图8 给出了补偿前后的波形结果。
3.57
其中，图中“A1”、“A2”、“A3”和“A4”表示制作缺陷
前后及经过不同温度补偿方法处理后的时域信号
௑ᫎ/(10 -4 s) 3.56 最大幅值，无缺陷和有缺陷两组实验信号所对应的

温度分别为21.1 C和14.5 C。
◦
◦
0.10
A4
3.55
0 10 20 30 40 50 60 70 80 90 A3
ࠄᰎ൓஝ 0.06
A2
(b) Ԡ᧚ t A
A1
图 6 监测实验中参量 E z、参量 t A 的变化趋势 ࣨϙ/V 0.02
Fig. 6 Change trend of parameters E z and t A in
monitoring experiments -0.02

进一步定量分析温度和参量 E z 、参量 t A 的关 B
-0.06 ௄Ꭵᬞ(21.1 Ć) ԠᏦ۳юᛪϪ(14.5 Ć)
系，结果如图 7 所示。转辙机构反射子波包能量值 Ꭵᬞ኎ጟ8(௄ᛪϪ 14.5 Ć) ಖࠀவሮᛪϪ(14.5 Ć)
1.0 1.1 1.2 1.3 1.4
E z 与温度近似线性相关，拟合方程为
ᡰሏ/m
E z (T) = (8.612T − 87.54) × 10 −3 , (2) 图 8 补偿前后的缺陷回波信号对比

Fig. 8 Comparison of defect echo signals before
0.14 3.58 and after compensation

在时间窗口 0.65 ∼ 0.85 ms 内统计波包能量
0.12
值。以无缺陷时该窗口波包能量值 E q 作为基准，
3.57 同时截取目标信号在该窗口的波包能量值 E q1 ，以
0.10
ᑟ᧚ϙ/V 2 ௑ᫎ/10 -4 s 增长率 β 来评价两种温度补偿方法的效果，其中

0.08 β = (E q1 − E q )/E q 。在标定方程补偿方法中，增长
3.56
率可表示为 β = (E q1 − E q /Q)/(E q /Q)。采用参考
2
R =0.3871
0.06 基准补偿后，目标信号在该窗口的波包能量值表示
为 E q2 ，则增长率为 β = (E q2 − E q )/E q 。如图 9 所
2
R =0.7488
0.04 3.55 示，基于标定方程的补偿方法对不同等级缺陷信号
14 18 22 26 14 18 22 26
ພए/Ć ພए/Ć 的补偿效果存在较大波动，例如第 3、第 4 等级缺陷
(a) Ԡ᧚E z (b) Ԡ᧚t A 信号补偿后 β 随缺陷等级增大而增大 (有利于缺陷
识别)，但第 5、第 6 等级缺陷信号补偿后 β 反而下
图 7 参量 E z、参量 t A 和温度的关系
降，也即补偿后缺陷信号的识别程度下降。这可以
Fig. 7 The relationship between parameter E z,
parameter t A and temperature 从图 6 所示的结果进行关联分析，主要原因是波包