Page 24 - 《应用声学》2023年第3期

462 2023 年 5 月

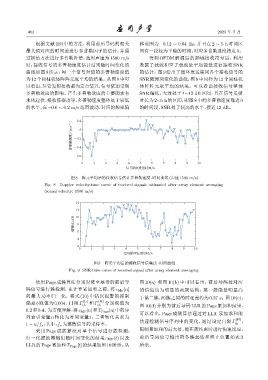
根据文献 [19] 中的方法，利用前后导码的相关 移范围为 −0.12 ∼ 0.04 Hz，并且在 2 ∼ 5 h 时间区
最大值对应的时间差进行多普勒因子的估计，并通 间有一段较为平稳的时期，对应多普勒速度接近0。
过插值方法进行多普勒补偿，选用声速为 1500 m/s 得到 OFDM 解调后的频域接收符号后，利用
时，接收信号的多普勒速度估计结果随时间变化的 数据子载波和空子载波处平均能量进行接收 SNR
曲线如图 8 所示，每一个信号对应的多普勒速度值 的估计。图9 给出了循环发送期间各个接收信号的
为12个圆柱状体阵阵元取平均的结果。从图8中可 SNR随时间变化的曲线，图9 中同样为 12个圆柱状
以看出，尽管发射接收都为定点装置，信号依旧受到 体阵阵元取平均的结果。可以看出接收信号整体
多普勒效应的影响。产生多普勒效应的主要因素有 SNR 偏低，大致处于 4∼12 dB 区间，且在信号发射
水体起伏、接收阵摆动等，多普勒速度整体处于较低 时长为2∼5 h的区间，即图8中的多普勒速度靠近0
的水平，在−0.6 ∼ 0.2 m/s范围波动，对应的频率偏 的时间段，SNR处于较高的水平，接近12 dB。

0.2
ܳ௿ҿᤴए/(mSs -1 ) -0.2 0

-0.4

-0.6
0 1 2 3 4 5 6 7 8 9 10
ηՂ॰ဗԧ᤟௑ᫎ/h

图 8 阵元平均后的接收信号估计多普勒速度 -时间曲线 (声速 1500 m/s)
Fig. 8 Doppler velocity-time curve of received signals estimated after array element averaging
(sound velocity: 1500 m/s)

14
12
η٪උ/dB 10 8 6

4
2
0 1 2 3 4 5 6 7 8 9 10
ηՂ॰ဗԧ᤟௑ᫎ/h
图 9 阵元平均后的接收信号信噪比 -时间曲线
Fig. 9 SNR-time curve of received signal after array element averaging

使用 Page 成簇算法分别对降至基带的前后导 图 10(a) 和图 10(b) 中可以看出，前后导码处对应

码信号进行簇检测，在计算累加和之前，将 c MF [n] 的信道均为明显的两簇结构，第一簇能量明显高
的最大功率归一化，将式 (10) 中错误报警的抑制 于第二簇，两簇之间的时延差约为0.37 s。图10(c)、
(L) (H)
偏差 b 取值为 0.004，门限 Γ th 和 Γ th 分别取值为 图 10(d) 分别为前后导码 LLR 的 Page 累加和结果，
0.2和0.4。为方便理解，将c MF [n]和T Page [n]中的序
可以看出，Page 成簇算法通过对 LLR 累加求和能
列索引变量 n 转化为时间变量 t，二者转化关系为
快速检测信号序列中的变化，通过设定门限 Γ (H) ，
t = n/f s ，其中，f s 为离散信号的采样率。 th
采用 Page 成簇算法对单个信号进行簇检测， 限制累加和的最大值，能在簇结束时进行快速反应。
归一化滤波器输出随时间变化的结果 c MF (t) 以及 前后导码信号输出的各簇起始和终止位置如表 3
LLR的Page累加和T Page [t]的结果如图10所示。从 所示。