Page 21 - 《应用声学》2023年第3期

第 42 卷 第 3 期 王悦悦等： 深海远程正交频分复用水声通信簇约束的分布式压缩感知信道估计 459

设定的迭代次数则停止迭代，并保存各数据块的多 为1/8，对应导频子载波数32个，导频子载波随机插
T
ˆ
ˆ T ˆ T
ˆ T T
径系数 ξ = [ξ , ξ , · · · , ξ ] ，其中 (·) 表示向量 入在 256 个子载波中，剩余的子载波用作数据子载
1 2 N
的转置；否则迭代继续进行，λ = λ + 1，接着执行步 波。发射信号具体参数见表1。
骤一到步骤三。
ˆ
输出：各通道的重构多径系数 ξ 和稀疏位置集 表 1 仿真所用发射信号参数
合θ。 Table 1 Transmit signal parameters used
ˆ
在确定了数据块的重构多径系数ξ 和稀疏位置 in the simulation
集合 θ 后，各个数据块对应的信道冲激响应估计值
参数 符号 仿真取值
ˆ 带宽 B 100 Hz
h i (i ∈ [1, N])也相应确定。
采用 CR-DCS 估计方法对水声信道进行估计 总子载波数目 L 256
时，利用了多个数据块信道的共同稀疏性，在SOMP 子载波间隔 ∆f 0.39 Hz
算法迭代中对数据块间多径位置相同的部分进行 导频子载波密度 L p/L 1/8
数据子载波数目 L data 224
叠加，联合确定多径稀疏解的位置，提高信道多径重
保护间隔长度 T g 2 s
构准确度，并引入簇区域约束矩阵，确定了有效字典 QAM 调制阶数 M 4
原子的范围，降低了噪声区域对估计结果的影响，进
一步提高了估计精度。 仿真所用信道模型来自实测数据提取的水声
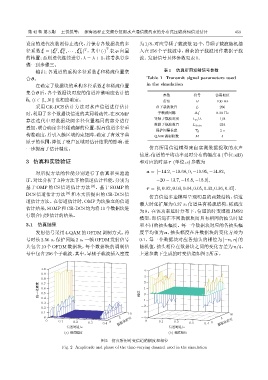
信道，信道的平均功率延时分布的幅度 ¯ a (单位：dB)
3 仿真和实验验证 和对应的时延τ (单位：s)参数为

对所提方法的性能分别进行了仿真和实验验 ¯ a = [−14.2, −10.68, 0, −10.95, −14.82,
证，对比分析了 3 种方法下的信道估计性能，分别为 −20 − 13.7, −16.8, −18.9],
基于 OMP 的 CS 信道估计方法 [6] 、基于 SOMP 的 τ = [0, 0.02, 0.03, 0.04, 0.05, 0.33, 0.36, 0.37].
DCS 信道估计方法 [8] 和本文所提出的 CR-DCS 信
仿真信道多途模型呈现明显的两簇结构，信道
道估计方法。在信道估计时，OMP为块独立的信道
最大时延扩展为 0.37 s，信道具有稀疏结构，稀疏度
估计结果，SOMP和CR-DCS均为将10个数据块进
为 9。在该功率延时分布下，信道的时变遵循 JMS2
行联合同步估计的结果。
模型，即信道在不同数据块间具有相同的抽头时延
3.1 仿真结果 和不同的抽头幅度。每一个数据块对应的各抽头幅
发射信号采用 4-QAM 的 OFDM 调制方式，符 度平均值为 ¯ a，抽头幅度在各数据块的变化方差为
号时长 2.56 s，保护间隔 2 s，一帧 OFDM 发射信号 0.1，每一个数据块对应各抽头的相位为 [−π, π] 的
共包含 10 个 OFDM 数据块，每个数据块的调制信 随机值，抽头相位在数据块之间的变化方差为 π/4。
号中包含256个子载波，其中，导频子载波插入密度 上述参数下生成的时变信道如图2所示。

1.0
4
0.9
3
0.8 2
0.7
ॆʷӑࣨए 0.6 ᄱͯ 1 0
0.5
0.4
-1
0.3
-2
0.2
0.1 10 -3 10
0 5 -4 5
0 0.1 0.2 0.3 0.4 0 ஝૶ڱጊळ 0 0.1 0.2 0.3 0.4 0 ஝૶ڱጊळ
η᥋௑ण/s η᥋௑ण/s
(a) η᥋ࣨए (b) η᥋ᄱͯ
图 2 仿真所用时变信道的幅度和相位
Fig. 2 Amplitude and phase of the time-varying channel used in the simulation