Page 88 - 《应用声学》2023年第4期

750 2023 年 7 月

1 2.2 仿真结果分析
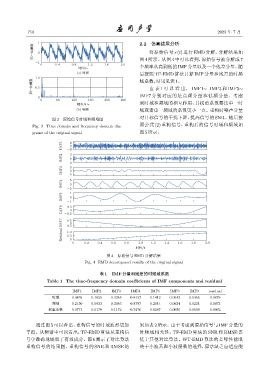
ॆʷӑࣨए 0 将原始信号 s (t) 进行 EMD 分解，分解结果如

-1 图 4 所示。从图 4 中可以看到，原始信号被分解成 7
0 0.4 0.8 1.2 1.6 2.0 个频率从高到低的IMF分量以及一个残差分量。随
௑ᫎ/s
(a) ௑۫ 后按照 TF-EMD 算法计算 IMF 分量和残差的时频
1.0 域系数，结果见表1。
ॆʷӑࣨए 0.5 由 表 1 可 以 看 出， IMF1∼ IMF3 和 IMF5∼

0 IMF7 分别对应的是高频分量和低频分量。考虑
0 50 100 150 200 250
ᮠဋ/Hz 到时域和频域的相互作用，其权重系数要比单一时
(b) ᮠ۫ 域或者单一频域的系数更小一点。重构时噪声分量
图 3 原始信号时域和频域图 对目标信号的干扰下降，提高信号的 SNR。随后按
Fig. 3 Time domain and frequency domain dia- 照公式 (2) 重构信号，重构后的信号时域和频域如
grams of the original signal 图5所示。

IMF1 -2 2 0

IMF2 -2 2 0

IMF3 -5 5 0

IMF4 5 0
-5
IMF5 1 0

-1
0.5
IMF6 -0.5 0
IMF7 -0.5 0
0.5
Residual 1.0
0.5
0
0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0
௑ᫎ/s
图 4 原始信号 EMD 分解结果
Fig. 4 EMD decomposed results of the original signal

表 1 IMF 分量和残差的时频域系数
Table 1 The time-frequency domain coefficients of IMF components and residual

IMF1 IMF2 IMF3 IMF4 IMF5 IMF6 IMF7 residual
时域 0.3435 0.1825 0.3255 0.8137 0.1412 0.0542 0.0355 0.0879
频域 0.2150 0.0933 0.3446 0.8797 0.2011 0.0634 0.0231 0.0673
权重系数 0.0771 0.0178 0.1172 0.7476 0.0297 0.0036 0.0009 0.0062

通过图 5 可以看出，重构信号的时域波形更加 果如表 2 所示。由于考虑到原始信号与IMF分量的
平滑。从频谱中可以看出，TF-EMD 算法从重构信 时频域相关性，TF-EMD 算法的 SNR 和 RMSE 要
号中准确地提取了有效成分。图 6 展示了对比算法 优于其他对比算法。WT-EMD 算法的去噪性能取
重构信号的结果图，重构信号的 SNR 和 RMSE 结 决于小波基和小波层数的选择，算法缺乏自适应能