Page 138 - 《应用声学）》2023年第5期

1030 2023 年 9 月

坐标系下补偿波束角度，再转换至笛卡尔坐标系下：
 -20
√
r 1 = h + y ,
 2 2
1 1
(17) ๒ງ/m -22
θ 1 = arctan (y 1 /h 1 ) ,

-24

r 2 = r 1 ,
 100
(18) 80
θ 2 = θ 1 +θ r ,
 60
40
 ෹ᓈᤜՔ x/m 50
y 2 = r 2 · sin θ 2 ,
 20 0
(19) 0 -50 ۇᄰᓈᤜՔ y/m
h 2 = r 2 · cos θ 2 .

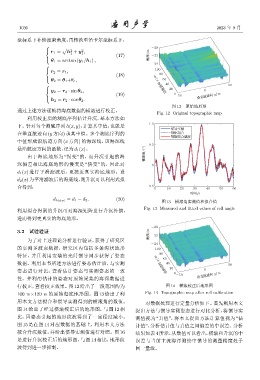
图 12 原始地形图
通过上述方法逐帧将海底数据的横滚进行校正。
Fig. 12 Original topographic map
利用校正后的测底序列估计升沉，基本方法如
下。针对每个测底序列h(x, y)，计算其中值，也就是 1.0
ਅ࠮ࠄ฾
在垂直航迹向 (y 方向) 求其中值。多个测底序列的 ஝૶લՌ
஝૶લՌ໚ฉ
中值形成沿航迹方向 (x 方向) 的海深线，该海深线
0.5
是沿航迹方向的函数，记为d 1 (x)。
由于海底地形为 “慢变” 的，而升沉引起的海 ഷ໔ᝈ/(O)
深偏差相比海底地形的慢变是 “快变” 的，因此对 0
d 1 (x) 进行平滑滤波后，更接近真实海底地形。设
d 2 (x)为平滑滤波后的海底线，则升沉可以利用式拟
合得到： -0.5 0 10 20 30 40 50 60
௑ᫎ/s
d heave = d 1 − d 2 . (20)
图 13 横滚角实测值和拟合值
利用拟合得到的升沉可对海深矩阵进行升沉补偿， Fig. 13 Measured and fitted values of roll angle
进而得到更真实的海底地形。

-20
3.2 试验验证 ๒ງ/m -22
为了对上述理论分析进行验证，获得了研究区
-24
的实测多波束数据，研究区内包括多条沟状地形 100
特征，并且利用安装的光纤惯导同步获得了姿态 80
෹ᓈᤜՔ x/m
60
数据。利用本节所述方法进行姿态估计后，与实测 40 50
姿态进行对比，查看估计姿态与实测姿态的一致 20 0
0
-50 ۇᄰᓈᤜՔ y/m
性。并利用估计的姿态对原始采集的海深数据进
行校正，查看校正效果。图12 给出了一段范围约为 图 14 横滚校正后地形图
100 m×120 m 的原始海底地形图。图 13 给出了利 Fig. 14 Topographic map after roll calibration
用本文方法拟合和惯导实测得到的横滚角的数值。 对数据处理进行定量分析如下。首先利用本文
图 14 给出了经过横滚校正后的地形图，与图 12 相 提出方法与惯导实测姿态进行对比分析，将惯导实
比，因姿态引起的地形纹波得到了一定程度减小。 测值视为 “真值”，将本文提出方法计算值视为 “估
图 15 是在图 14 对应数据的基础上，利用本文方法 计值”，分析估计值与真值之间偏差的中误差。分析
拟合升沉数值，并给出惯导实测值进行对照。图 16 结果如表4所示，从数值可以看出，横滚和升沉的中
是进行升沉校正后的地形图，与图 14 相比，地形纹 误差与当前主流海洋测绘中惯导的测量精度处于
波得到进一步抑制。 同一量级。