Page 158 - 《应用声学》2023年第6期

1268 2023 年 11 月

设置为硬声场边界，吸声柱两端导流罩设置为内部 果见表 4。由表 4 可知，不同阵列式消声器各倍频带
硬声场边界。入射声场设置背景压力场，压力场类 消声量修正系数相近，故取算术平均值作为各倍频
型为平面波，声压幅值为 1 Pa，入射方向为垂直入 带消声量修正系数。
射。当声源激发频率高于管道的截止频率，管道中 由表 4 可知，各倍频带消声量修正系数随频率
会存在大量的高阶模态声波，此时管道内的声场是 升高先增大后减小，在1000 Hz 处达到峰值，整体呈
各个模态叠加的稳态声场。 现中间高两边低的特点，类似高斯分布。采用高斯
2.1.4 网格划分 分布函数对各倍频带消声量修正系数进行拟合 (见
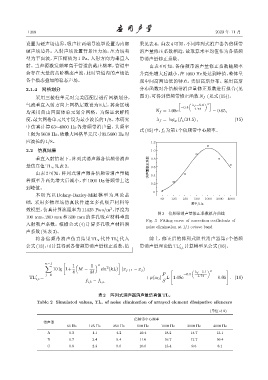
采用三棱柱单元对完美匹配层进行网格划分， 图3)，可得到倍频带修正函数N f (见式(15))。
气流垂直入射方向上网格层数设为 8 层，其余区域 [ ( λ f −5.1 ) ]
2
−0.5 1.74
均采用自由四面体单元划分网格。为保证求解精 N f = 1.08e − 0.05,
度，最大网格单元尺寸设为最小波长的1/8。本研究 λ f = log (f i /31.5) , (15)
2
中仿真计算 63∼4000 Hz 各倍频带消声量，其频率
式(15)中，f i 为第i个倍频带中心频率。
上限为5600 Hz，故最大网格单元尺寸取5600 Hz对
应波长的1/8。 1.2

2.2 仿真结果 1.0
垂直入射情况下，阵列式消声器各倍频带消声 0.8
量仿真值TL s 见表 2。 ๗ܦ᧚ξ൤ጇ஝ 0.6
由表 2 可知，阵列式消声器各倍频带消声量随 0.4
着频率升高先增大后减小，在 1000 Hz 倍频带上达
0.2
到峰值。
0
本研究以 Delany-Bazley-Miki 模型为理论基
63 125 250 500 1000 2000 4000
础，采用多物理场仿真软件建立多孔吸声材料等 ᮠဋ/Hz
2
效模型，仿真计算流阻率为 11425 Pa·s/m ，厚度为
图 3 倍频带消声量修正系数拟合曲线
100 mm、200 mm 和 300 mm 的多孔吸声材料垂直
Fig. 3 Fitting curve of correction coefficients of
入射吸声系数。根据公式 (4) 计算多孔吸声材料消
noise elimination at 1/1 octave band
声系数(见表3)。
将各倍频带消声仿真结果 TL s 代替 TL 代入 综上，修正后的阵列式阻性消声器第 i 个倍频
′
t
公式(13)，可计算得到各倍频带消声量修正系数，结 带消声量理论值TL ′ 计算模型见公式(16)。
t,i

n−1 [ ]
∑ 1 ( 1 ) 2 2
10 lg 1+ M − sin (kL) (x j+1 − x j ) [ ( ) ]
4 M λ f −5.1 2
j=0 P −0.5 1.74
′
TL = +φ(α 0 ) L 1.08e − 0.05 . (16)
t,i
f i,b − f i,a S
表 2 阵列式消声器消声量仿真值 TL s
Table 2 Simulated values, TL s of noise elimination of arrayed element dissipative silencers

(单位：dB)
倍频带中心频率
消声器
63 Hz 125 Hz 250 Hz 500 Hz 1000 Hz 2000 Hz 4000 Hz
A 0.3 1.1 4.2 10.4 18.2 14.7 13.1
B 0.7 2.4 5.4 11.6 16.7 12.7 10.4
C 0.8 2.3 5.0 10.0 13.4 9.6 8.1