Page 181 - 《应用声学》2023年第6期

第 42 卷 第 6 期 赵晓静等： 基于频谱 Sevcik 维数的目标运动速度估计 1291

其中，(x , y )是信号波形上一系列点归一化后的结
∗
∗
k
k
果，x 、y 表达式如下：
∗
∗
610 k k
x k y k − y min
∗
x = , y = . (5)
∗
k
ᮠဋ/Hz 对于一个时域信号 s(t)，若其时长为 T，采样率
k
600
x max
y max
590
为 f s ，信号点个数为 N，则其经过快速傅里叶变换
(Fast Fourier transform, FFT) 后，频谱 S(f) 的 x k
580
2 4 6 8 对应信号频率点f k 。此时其信号波形长度 L的表达
௑ᫎ/s
(a) ଌஆηՂLOFARڏ 式经整理后如式(6)所示：
√
N−2
∑ 1 ( ) 2
L = + S k+1 − S k ∗ , (6)
∗
610 (Tf s ) 2
k=1
其中，S 是S(f)取模幅度值S k 归一化后的结果。将
∗
k
ᮠဋ/Hz 600 式(6)代入式(3) 即可求得信号频谱的Sevcik维数。
590 1.3 算法步骤
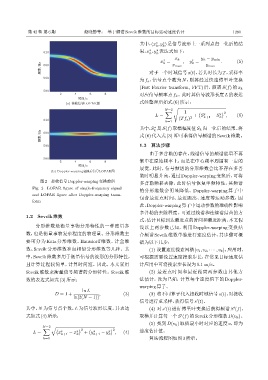
由于多普勒的存在，线谱信号的频谱能量不再
580
2 4 6 8 集中在原始频率上，而是在中心频率周围有一定的
௑ᫎ/s
展宽，此时，信号频谱的分形维数会比不存在多普
(b) Doppler-warpingԫ૱ՑηՂLOFARڏ
勒时明显升高，通过 Doppler-warping 变换后，可将
图 2 接收信号 Doppler-warping 变换前后 多普勒频移去除，此时信号恢复单频特性，其频谱
Fig. 2 LOFAR figure of single-frequency signal
的分形维数会明显降低。Doppler-warping 算子中
and LOFAR figure after Doppler-warping trans-
包含最近点时间、最近距离、速度等运动参数，因
form
此，Doppler-warping算子中运动参数的准确性影响
多普勒的去除程度。可通过线谱和连续谱结合的方
1.2 Sevcik维数
式，估计目标到达最近点的时间和最近距离，本文假
分形维数是衡量事物分形特性的一种度量参 设以上两参数已知，利用 Doppler-warping 变换结
数，也是衡量事物复杂程度的物理量。分形维数主 合频谱 Sevcik 维数单独进行速度估计，其步骤可概
要可分为 Katz 分形维数、Hausdorff 维数、计盒维 括为以下几步：
数、Sevcik 分形维数和自相似分形维数等几种。其 (1) 设置速度搜索网格[v 1 , v 2 , · · · , v k ]。应用时，
中，Sevcik 维数多用于衡量信号的波形的分形特性， 可根据需要设置速度搜索步长，在常见目标速度估
且计算过程较简单，计算时间短。因此，本文采用 计应用中可将搜索步长设为0.1 m/s。

Sevcik 维数来衡量信号频谱的分形特性。Sevcik 维 (2) 最近点时间和最近距离两参数由其他方
数的表达式如式(3)所示： 法估计，设为已知，计算每个速度值下的 Doppler-
warping算子。
ln L
D = 1 + , (3) (3) 将不同算子代入接收时域信号s(t)，对接收
ln[2(N − 1)]
信号进行重采样，获得信号s (t)。
′
其中，N 为信号点个数，L 为信号波形长度，其表达 (4) 对 s (t) 进行傅里叶变换后获得频谱 S (f)，
′
′
式如式(4)所示： 取模并计算每一个S (f)的Sevcik分形维数D(v k )。
′
(5) 找到 D(v k ) 取值最小时对应的速度 v，即为
N−2 √
∑ ( ) 2 ( ) 2 速度估计值。
L = x ∗ − x ∗ + y ∗ − y ∗ , (4)
k+1 k k+1 k
k=1 算法流程图如图3所示。